... student: Oblicz pole obszaru ograniczone y=x², y=1/2x², y=3x

Jack:

	x2
3x,		, x2
	2

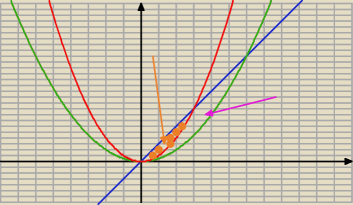
tak wyglada rys. o ktory obszar chodzi ? ten brazowy? to wtedy x²/2 nie ma sensu bytu a jezeli ten rozowy (bez brazowego) to x² nie ma sensu chyba ze o calosc chodzi...

aniabb: różowy bez brązowego używa wszystkich trzech do całości nie potrzeba x²

Jack: nah, no dobra

Mila: wolfram tak policzył: http://www.wolframalpha.com/input/?i=area+between+y%3Dx%5E2,+y%3D1%2F2x%5E2,+y%3D3x

aniabb: wolfram nie uwzględnił x²

aniabb: od 0 do 3 ∫x²−x²/2 dx + od 3 do 6 ∫3x−x² dx

Jack: obszar trzeba podzielic na 2. 1) granice od 0 do przeciecia y=3x i y= x² (oczywiscie mowie o tym iksie roznym od 0) z funkcji (x² − 1/3x²) 2) granice calkowania od tej gornej poprzedniej do przeciecia 3x i 1/3x² z funkcji (3x−1/3x²)

Mila: Tak jak Ania 21:44.

student: A można zrobić tak, że od 0 do 6 (3x−x²/2) − od 0 do 3 (3x−x²)?

Mila: 1)

	1		1
P1=∫03(x2−		x2)dx=		*∫03(x2 )dx=
	2		2

	1		9
=[		x3]03=
	6		2

	1		3		1
P2=∫36(3x−		x2) dx=[		x2−		x3]36=9
	2		2		6

P=4.5+9=13.5 II sposób

	1		3		1
P1=∫06(3x−		x2) dx =[		x2−		x3]06=
	2		2		6

	3		1
=		*62−		*63=18
	2		6

	3		1
P2=∫03(3x−x2) dx=[[		x2−		x3]03=
	2		3

	3		1		27
=		*32−		*33=		−9=4.5
	2		3		2

P=18−4.5=13.5 Drugi sposób łatwiejszy do rachunków.