Proste zadanko 123: Dla jakich wartości parametru a równanie ||x|−2+a|=3 ma dokładnie trzy pierwiastki? Proszę o założenia, czyli co musi spełniać a, bo mam chyba chwilowe zaćmienie...

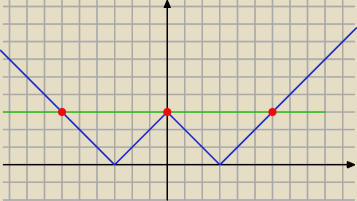
aniabb: dla a =−1

123: Dziękuję, znam rozwiązanie, ale czy warunki (5−a>0 i −a−1=0) lub (5−a=0 i −1−a>0) wynikają po prostu z definicji modułu przy x?

123: Proszę o wytłumaczenie dlaczego tych równań: |x|=5−a lub |x|=−a−1 nie rozbijamy na kolejne dwa, tylko wyciągamy te warunki?

aniabb: bo jak widać na obrazku jedno ma dawać dwa rozwiązania, a drugie jedno ... żeby były trzy

aniabb: wynikają z treści zadania

123: Rozumiem, że na obrazku widać, ale jeśli rozwiązuję zadania bez obrazka. Zwyczajnie nie rozumiem powodu, że w tym momencie są takie warunki, a nie dalsze rozbijanie modułów?

Jerzy: |x| = A lub |x| = B Aby istniały tylko trzy rozwiazania, to: 1) A > 0 i B = 0 lub 2) A = 0 i B > 0

aniabb: bo tylko | | =0 daje jedno rozwiązanie a Ty masz taki warunek że masz mieć 3 rozwiązania więc z tych dwóch przypadków jedno musi być zerowe a drugie dodatnie (kolejne dwa) żeby były 3 chcesz znaleźć parametr, a nie rozwiązać równanie i dlatego nie liczysz dalej

123: Bardzo dziękuję, o to chodziło. Jeśli jeszcze mógłbym prosić link do strony, gdzie są wypisane te warunki, ewentualnie dział?

aniabb: jak piszę krótko to za krótko..jak długo to się okazuje że niepotrzebnie

aniabb: https://matematykaszkolna.pl/strona/3410.html

aniabb: a warunki masz w treści zadania więc raczej takiej strony nie znajdziesz jedyne co trzeba wiedzieć to że 0 nie ma znaku, więc jest jako jedyne jedno

123: Dziękuję Pani za pomoc, chociaz bardziej do mnie trafiło wyjaśnienia Jerzego.

aniabb: bo to co napisał Jerzy było dokładnie tym samym co Ty miałeś napisane o 17:25 to skoro to rozumiałeś to po co pytałeś?

123: Pytałem bo nie rozumiałem, ale chciałbym wiedzieć skąd Państwo znacie te warunki, gdzie one są wypisane?

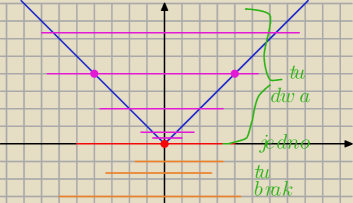
aniabb: znasz wykres funkcji |x| jak poprowadzisz poziomą kreskę to przetnie się w jednym miejscu tylko na czubku ... czyli dla y=0 i to jest to jedno rozwiązanie więc jak wyszło Ci |x| = A lub |x| = B to jedno z nich musi być równe zero żeby było 1 rozwiązanie .. a drugie dodatnie żeby były kolejne dwa rozwiązania

aniabb: i zależnie od treści zadania składasz te rozwiązania...

123: Ok, teraz już rozumiem, bardzo Pani dziękuję