PW: Krzysiu, jeżeli podane odcinki mają być wysokościami jednego trójkąta, to zadanie jest
trudne, powstaje pytanie czy taki trójkąt w ogóle istnieje.
anaisy:
Załóżmy, że mamy odcinki h
a, h
b, h
c i są wysokościami pewnego trójkąta ABC odpowiednio na
boki a, b, c)
Spróbujmy narysować sobie jakiś trójkąt podobny do tego trójkąta o bokach a', b', c'
(standardowe oznaczenia)
Taki trójkąt miałby wysokości h
a', h
b', h
c', takie, że
Więc jak to zrobić. Bierzemy sobie odcinek dowolnej długości i załóżmy, że to będzie a'.
To teraz poszukajmy długość boku b'. Mamy h
a'*a'=h
b'*b' (bo pole) czyli też h
a*a'=b
b*b' (bo
poprzedni ciąg równości)
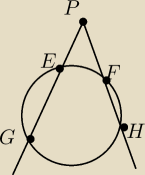
Rozważmy kąt ostry EPF, przy czym PE=h
a i PF=h
b. Na półprostej PE zaznaczamy G, taki, że
PG=a'.
Opisujemy okrąg na EGF, załóżmy, że przecina on PF w H róźnym od F (gdy jest styczny do PF, to
H=F)
Wtedy PH=b'. Analogicznie konstruujemy odcinek c'. Teraz trójkąt o bokach a', b', c'. Rysujemy
jego wysokości,
bierzemy najkrótszą jego wysokość, teraz przedłużamy/skracamy ją do najkrótszej z wysokości
h
a, h
b, h
c i w odpowiednim
punkcie na tej wysokości rysujemy prostą do niej prostopadłą i mamy trójkąt podobny do tego o
bokach a', b', c' tylko o bokach a, b, c

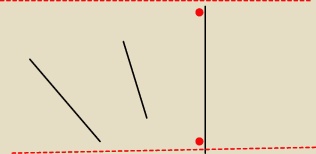 Narysowane odcinki to wysokosci pewnego trojkata
Narysuj ten trojkat
Do tej pionowej wysokoci to narysowalem (albo tu albo tu bok
Narysowane odcinki to wysokosci pewnego trojkata
Narysuj ten trojkat
Do tej pionowej wysokoci to narysowalem (albo tu albo tu bok
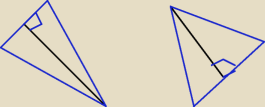
 Dobry wieczor PW
Dobry wieczor PW  Ono jest oznaczone jako trudne i tak sie zastanawiam jak to mlodemu wytlumaczyc .
Ono jest oznaczone jako trudne i tak sie zastanawiam jak to mlodemu wytlumaczyc .

 Załóżmy, że mamy odcinki ha, hb, hc i są wysokościami pewnego trójkąta ABC odpowiednio na
boki a, b, c)
Spróbujmy narysować sobie jakiś trójkąt podobny do tego trójkąta o bokach a', b', c'
(standardowe oznaczenia)
Taki trójkąt miałby wysokości ha', hb', hc', takie, że
Załóżmy, że mamy odcinki ha, hb, hc i są wysokościami pewnego trójkąta ABC odpowiednio na
boki a, b, c)
Spróbujmy narysować sobie jakiś trójkąt podobny do tego trójkąta o bokach a', b', c'
(standardowe oznaczenia)
Taki trójkąt miałby wysokości ha', hb', hc', takie, że

