ostrosłup prosty Szczeniak: Podstawą ostrosłupa jest trapez równoramienny o kącie ostrym α, w którym ramię i krótsza podstawa ma długość a. Każda krawędź boczna ostrosłupa tworzy z płaszczyzną podstawy kąt β. Oblicz objętość tego ostrosłupa. Jak wygląda ten ostrosłup, potrafi ktoś narysować? Skoro każda krawędź boczna tworzy z płaszczyzną podstawy taki sam kąt to spodek wysokości bryły musi być środkiem okręgu opisanego na podsatwie czyli tym trapezie równoramiennym. Gdzie ten środek narysować? Poza trapezem, na środku dłuższej podsatwy czy wewnątrz figury? Z góry dziękuję

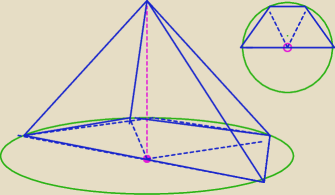
ite: spodek wysokości bryły jest środkiem okręgu opisanego na trapezie i leży w połowie dłuższej podstawy

ite: teraz zauważyłam, że zrobiłam błędne założenie, że α=60^o tak oczywiście nie musi być rysunek nie jest właściwy

Szczeniak: Czy ten trapez jest zbudowany z trzech trójkątów równobocznych o boku długości promienia okregu opisanego na nim?

Szczeniak: Ok

Szczeniak: pomoże ktoś?

Szczeniak: Zadanie jest do rozwiązania i bez tego, ale nurtuje mnie to nadal, od czego zależy połozenie środka okręgu opisanego na trapezie równoramiennym

dero2005: https://matematykaszkolna.pl/forum/372414.html

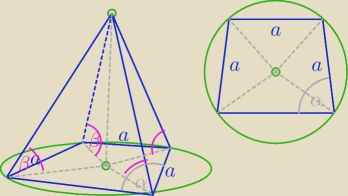
iteRacj@: @dero2005 czy taka sytuacja, jak na tym rysunku jest możliwa i zgodna z warunkami zadania?

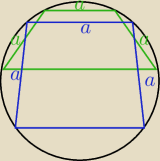
dero2005: Tak, jest możliwa i zgodna z warunkami zadania, tylko że z tego zadania nie obliczysz objętości, bo pole podstawy może przyjmować różne dowolne wartości. (Patrz rysunek) Ja nawiązywałem do zadania, w którym środek koła opisanego leży w połowie dłuższej podstawy. Wtedy warunek jest jednoznaczny i można obliczyć objętość

iteRacj@: dziękuję za wyjaśnienie

iteRacj@: @dero2005 moich przemyśleń ciąg dalszy pole trapezu z 18:58 można obliczyć i wynosi ono a²(1+cos α)sin α, podany w zadaniu kąt i długość boku wyznaczają pole jednoznacznie, czy rzeczywiście tak jest?

aniabb: tak

dero2005: Przyznaję, że niedokładnie przeczytałem treść zadania i przeoczyłem ten kąt α.

iteRacj@: dziękuję Wam za odpowiedzi