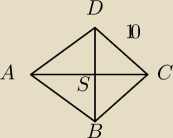
geometria analityczna dan: Punkty A(2,−6),C(4,8) są przeciwległymi wierzchołkami rombu ABCD o boku długosci 10.Wyznacz wspolrzedne pozostalych wierzcholkow tego rombu. Zatem wiemy ze |CD|=10,S=(3,1). |SC|=√1+49=√50 i z trojkata DSC pitagoras −> |DS|=√50

DS
	=1 −> tg45=1
SC

wiec prosta DC ma postac y=x+b,nalezy do niej punkt C wiec 8=4+b b=4 y=x+4 −> prosta DC Wiemy ze punkt D nalezy na prostej y=x+4 wiec jego wspolrzedne to (x,x+4). Odleglosc punktu S od D wynosi √50 wiec wzor na odleglosc punktu od drugiego punktu (x−3)²+(x+3)²=50 x1=4 x2=−4 y1=8 y2=0 Ale nie zgadza sie bo w odpowiedziach jest (−4,2) albo (10,0) (nie wiem ktore do punktu D lub B). Czy powinienem to policzyc inaczej?np. |CS|=|SD| i z tego obliczyc?

jc: Układ równań (x−4)²+(y−8)²=100 (x−2)²+(y+6)²=100 ma dwa rozwiązania: (x,y)=(−4,2), (10,0) Przy okazji, skąd wziąłeś taką staroświecką notację A(2,−6) zamiast A=(2,−6)? Jak w tej notacji zapiszesz (A−B)²=100? (A(2,−6)−B( , ))²=100? Co wpiszesz przy B?

dan: nie wzialem,po prostu kwestia lenistwa.Skad Ci sie wzial punkt (4,8) i (2,−6)?

dan: a byl podany no tak juz zapomnialem tresc zadania,dzieki