| 1 | cosx | sinx | |||
− tgx = ctgx − tgx = | − | ||||
| tgx | sinx | cosx |
| 8 | 15 | |||
skoro sinx = | to cosx = | |||
| 17 | 17 |
| sin2x | 1−cos2x | (1−cosx)(1+cosx) | |||
= | = | = 1 − cosx | |||
| 1+cosx | 1+cosx | 1+cosx |
| 8 | 225 | 15 | ||||
cosx= √1−sin2x= √1−( | )2= √ | = | ||||
| 17 | 289 | 17 |
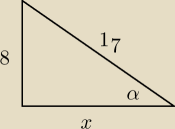Dla kąta ostrego łatwiej posłużyć się trójkątem prostokątnym:
x2+82=172
x2=289−64
x2=225
x=15
| 8 | 1 | 15 | ||||
tgα= | , | = | ||||
| 15 | tgα | 8 |
| 1 | 15 | 8 | 225−64 | 161 | |||||
−tgα= | − | = | = | ||||||
| tgα | 8 | 15 | 120 | 120 |