Przekroje Janek: Kwadrat ABCD o boku długości a jest podstawą ostrosłupa ABCDS. Krawędz boczna AS ma również długość a i jest prostopadła do płaszczyzny podstawy. Ostrosłup ten przecięto płaszczyną przechodzącą przez wierzchołek A i prostopadłą do krawędzi CS. Oblicz pole otrzymanego przekroju. Będzie to deltoid jak się nie mylę, jedna przekątna policzyłem z pół trójkątów i otrzymałem : √6/3 *a Jak drugą przekątna wyliczyć Czy ona będzie będzie połowa przekątnej podstawy?

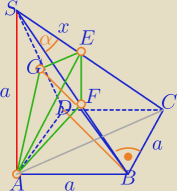
Mila: GF||DB AE⊥SC, |SB|=a√2 1)

	1		a2√2
PΔSAC=		*a*a√2=
	2		2

|SC|²=a²+(a√2)²=3a² |SC|=a√3

	1		a√3
PΔSAC=		*|SC|*|AE|=		*|AE|
	2		2

a√3		a2√2
	*|AE|=
2		2

	a√6
|AE|=
	3

2) W ΔAES:

	a√6
a2=x2+(		)2
	3

	2
a2−		a2=x2
	3

	a		a√3
x=		=
	√3		3

	√2
W ΔSBC: cosα=
	√3

	x
W ΔSEF: cosα=
	SF

	a√2
|SF|=		− Punkt F jest w połowie SB
	2

3)

	1		a√2
|GF|=		|BD|=
	2		2

Pewnie jest jeszcze inny sposób zauważenia tego faktu. 4)

	a2√3
P=
	6

============ JUtro popatrzę, jeśli to będzie kogoś interesowało.