geometria
Franklin p_p: W czworokącie wypukłym ABCD wpisanym w okrąg miary dwóch kolejnych kątów wynoszą α oraz 90+α,
gdzie α∊(0,90).
Wykaż że jeśli sin(α+45) = 2√2/3 to suma długości przekątnych tego czworokąta jest równa 8/3 R,
gdzie R to promień okregu opisanego na tym czworokącie.
Sam zrobiłem tyle: Kolejne kąty to α, 90+α, 180−α, 90−α.
27 mar 21:15
Franklin p_p: | | 4 | |
Ok korzystając z sin(α+45)= .... doszedłem do sinα + cosα= |
| |
| | 3 | |
27 mar 21:30
Eta:
No i ok

Teraz z tw. sinusów
d
1=2Rsinα
d
2=2Rcosα
d
1+d
2=2R(sinα+cosα)=........... teza

27 mar 21:37
27 mar 21:38
Eta:
po co?
27 mar 21:39
Franklin p_p: a już nic, nie widziałem twojego postu

27 mar 21:40
Eta:

27 mar 21:40
Eta:
W takim razie ... "dziękuję"

27 mar 21:42
Franklin p_p: Dziękuję bardzo

A chętna na jeszcze jkedno z geometrii? W którym chyba daleko zaszedłem ale
nie wiem co dalej i nei wiem czy dobrze działam

27 mar 21:43
Basia:
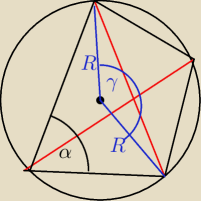
dołóż jedynkę trygonometryczną i wylicz sin α i cos α
y=2α
wylicz cos(2α) i skorzystaj z tw.cosinusów do policzenia d
2
drugą przekątną analogicznie korzystając z kata 90−α i środkowego 180−2α
27 mar 21:44
Eta:
Wpisuj .... ( jak wypiję herbatkę to zerknę

27 mar 21:44
Eta:
No to już masz następnego chętnego czyli
Basię 
Pozdrawiam
Basię
27 mar 21:46
Franklin p_p: Dziękuję Basiu za 2 sposób

Właśnie do tego dążyłem, ale Eta pokazała drogę na skróty

27 mar 21:46
Franklin p_p: W Trapezie ABCD AB || DC oraz |AB\ > |DC|
Na podstawie DC wybrano punkt M w taki sposób
,że |DM| : |MC|= 9 : 16. Prosta AM przecina przedłużenie ramienia BC w punkcie E. Punkt P jest
| | 1 | |
punktem wspólnym przekątnej BD i odcinka AE. Wykaż, że jeśli |AP|=|ME| to |PM|= |
| |AP |
| | 4 | |
Zaraz postaram się zrobić rysunek na forum

27 mar 21:50
Franklin p_p:
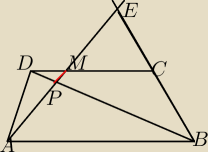
27 mar 21:53
Franklin p_p: Tak więc nie wiem czy mogę tak zrobić ale zakładam, że Teza jest prawdziwa, czyli podstawiam
tam x i jadę z Talesa, wykazuje, że |AB| = 36y, przy oznaczeniach, że |DM|=9y |MC|=16y |ME|=4x
| | 4x | | 9x | |
|MP|=x |AP|=4x czyli z Talesa mam |
| = |
| => |AB|=36y |
| | 16y | | |AB| | |
Poprowadziłem także prostą równoległą do AE od wierzchołka C, która przecina mi podstawę AB w
punkcie K oraz prostąDB w puncie G. powstaje mi równoległobok |AK|=16y |KB|=20y |CK|=5x i co
dalej. Wiem, że trójkąty DMP i CDG są podobne
27 mar 21:58
Eta:
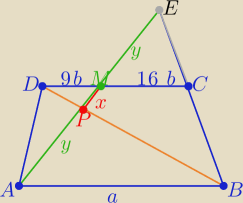
Z podobieństwa ΔABE i MCE z cechy(kkk)
| a | | 2y+x | |
| = |
| ⇒ ay=16b(2y+x) |
| 16b | | y | |
i z podobieństwa ΔABP i PMD
dzieląc stronami obydwa równania:
otrzymujemy:
| y | | 16(2y+x) | |
| = |
| ⇒ ...................................... |
| x | | 9y | |
16x
2+32yx−9y
2=0 Δ x= 1600y
2 i x>0
i mamy tezę
===========
27 mar 22:41
Franklin p_p: Zaraz przeanalizuję, dziękuje

27 mar 22:55
 Teraz z tw. sinusów
d1=2Rsinα
d2=2Rcosα
d1+d2=2R(sinα+cosα)=........... teza
Teraz z tw. sinusów
d1=2Rsinα
d2=2Rcosα
d1+d2=2R(sinα+cosα)=........... teza




 A chętna na jeszcze jkedno z geometrii? W którym chyba daleko zaszedłem ale
nie wiem co dalej i nei wiem czy dobrze działam
A chętna na jeszcze jkedno z geometrii? W którym chyba daleko zaszedłem ale
nie wiem co dalej i nei wiem czy dobrze działam
 dołóż jedynkę trygonometryczną i wylicz sin α i cos α
y=2α
wylicz cos(2α) i skorzystaj z tw.cosinusów do policzenia d2
drugą przekątną analogicznie korzystając z kata 90−α i środkowego 180−2α
dołóż jedynkę trygonometryczną i wylicz sin α i cos α
y=2α
wylicz cos(2α) i skorzystaj z tw.cosinusów do policzenia d2
drugą przekątną analogicznie korzystając z kata 90−α i środkowego 180−2α

 Pozdrawiam Basię
Pozdrawiam Basię
 Właśnie do tego dążyłem, ale Eta pokazała drogę na skróty
Właśnie do tego dążyłem, ale Eta pokazała drogę na skróty 


 Z podobieństwa ΔABE i MCE z cechy(kkk)
Z podobieństwa ΔABE i MCE z cechy(kkk)
