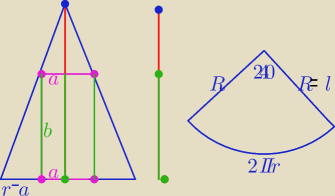
Rozpatrujemy wszystkie walce wpisane w stożek. Hesoyam: Rozpatrujemy wszystkie walce wpisane w stożek, którego powierzchnia boczna jest wycinkiem koła o promieniu R i kącie środkowym 240(stopni). Oblicz pole powierzchni całkowitej tego walca, którego objętość jest największa. Wyznacz stosunek objętości otrzymanego walca do objętości stożka.

Hesoyam: :(

Eta:

240		2πr		2		√5R
	=		⇒ r=		R to H=√R2−r2=
360		2πR		3		3

wymiary walca : a−− dł. promienia podstawy , b −− dł. wysokości z podobieństwa trójkątów

r−a		r		R√5		a√5
	=		⇒.................. b=		−
b		H		3		2

V_w=πa²*b

	π√5a2
V(a)=		(2R−3a)
	6

	π√5
V(a)=		(−3a3+2Ra2)
	6

V^'(a)..... V^'(a)=0 ⇒ −9a²+4Ra=0 ⇒ a=4R/9 to b=............ ........... określ czy to jest maximum ................ dokończ .......................... ......................