Sprawdzianik Maciess: Na sprawdzianie będę miał rysowanie wykresów funkcji wiec szybkie pytanie bo zawsze mi się myli f(x)=log _c (|x|−1) Tutaj najpierw wykonuje y=f( |x| ) a potem przesuwam o wektor log _c ( |x−1| ) Tutaj najpierw przesuwam o wektor a potem wykonuje y=f( |x| ) Dobrze?

Pawiuszek: jest ok chyba

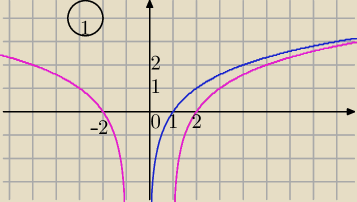
Mila: 1)y= log₂(x) →T_[1,0]⇒ 2) y=log₂(x−1) i teraz symetria względem OY⇒ y=log₂(|x|−1)

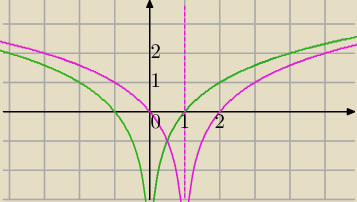
Mila: y=log c ( |x−1| ) Druga funkcja: y=log ₂ ( |x−1| ) 1)y=log₂x symetria względem OY⇒ 2) y=log₂(|x|)→T_[1,0]⇒ y=log₂(|x−1|} Jeżeli najpierw przesuniesz o wektor [ 1,0] to dalej będzie symetria względem prostej x=1 . Sprawdzaj na wykresie miejsce zerowe i f(0) jeśli 0 należy do dziedziny funkcji. log₂(|x−1|)=0 log₂(|x−1|)=log₂(1) |x−1|=1 x−1=1 lub x−1=−1 x=2 lub x=0 f(0)=log₂(|0−1|)=log₂(1)=0

Maciess: Dziękuje bardzo Milu, postaram się nie pomylić

Mila: Powodzenia. Nie wiem, po co Was męczą tymi przekształceniami wykresów.

PW: Albowiem to bardzo ważne i przydatne jest