pomocy :( aga: W układzie współrzędnych dane są punkty A(−4, −1) B(−2, 3) C(2, −3) D(5,3) a) wykaż, że AB ∥ CD b) wyznacz środek i skalę jednokładności przekształcającej odcinek AB na CD. Rozważ dwa przypadki

the foxi: a) Współczynnik kierunkowy a₁ prostej przechodzacej przez odcinek AB musi być równy współczynnikowi a₂ prostej przechodzącej przez CD

	3−(−1)
a1=		=2
	−2−(−4)

	3−(−3)
a2=		=2
	5−2

a₁=a₂ co należało wykazać

aga: A b) jak zrobić?

the foxi: Nie mam pojęcia, może ktoś inny odwiedzi Twój temat.

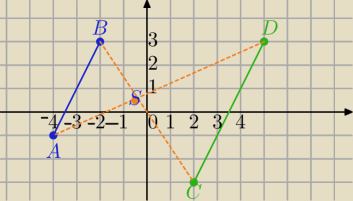
Mila: A(−4, −1), B(−2, 3), C(2, −3) ,D(5,3) a) AB^→=[2,4], CD^→=[3,6]

2		4		2
	=		=		⇔wektory sa równoległe⇔AB||CD
3		6		3

b) skala:

	3
|k|=|		| albo liczysz długości odcinków
	2

	3		3
k=		lub k=−
	2		2

	3
b1)S(x,y) − środek jednokładności i k=−
	2

z definicji: SD^→=k*SA^→ SD^→=[5−x,3−y] SA^→=[−4−x,−1−y]

	3
[5−x,3−y] =−		*[−4−x,−1−y]
	2

	3		3
5−x=		*(4+x) i 3−y=		*(1+y)
	2		2

	−2
x=		, y=U{3}{5)
	5

	−2		3
S=(		,		)
	5		5

b2)

	3
k=		, S'(x,y)− środek jednokładności
	2

	3
SC→=		*SA→
	2

Na drugim rysunku, chyba, że sama już zrobisz?