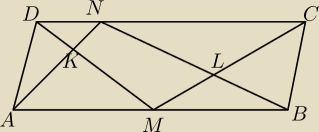
 Punkty M i N leżą odpowiednio na bokach AB i CD równoległoboku ABCD. Odcinki AN i DM przecinają
się w punkcie K, zaś odcinki BN i CM w punkcie L. Wykaż że pole czworokąta KMLN jest równe
sumie pół trójkątów AKD i BCL
Punkty M i N leżą odpowiednio na bokach AB i CD równoległoboku ABCD. Odcinki AN i DM przecinają
się w punkcie K, zaś odcinki BN i CM w punkcie L. Wykaż że pole czworokąta KMLN jest równe
sumie pół trójkątów AKD i BCL
| 1 | ||
PABN=|AB|*h* | ||
| 2 |
| 1 | ||
PMBC=|MB|*h* | ||
| 2 |
| 1 | ||
PADM=|AM|*h* | ||
| 2 |
| 1 | 1 | 1 | ||||
PMBC+PADM=|MB|*h* | +|AM|*h* | =|AB|*h* | ||||
| 2 | 2 | 2 |
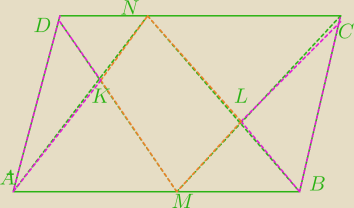
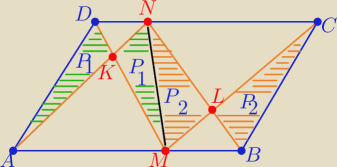 Zauważyć podział odcinkiem MN na dwa trapezy
w których pola P1 są równe i pola P2 są równe
zatem
P(KLMN)= P1+P2= P(AKD)+P(BCL)
c.n.w
Zauważyć podział odcinkiem MN na dwa trapezy
w których pola P1 są równe i pola P2 są równe
zatem
P(KLMN)= P1+P2= P(AKD)+P(BCL)
c.n.w