Pytający:
Hasło klucz: "zasada włączeń i wyłączeń". Możesz poszukać i poczytać, jeśli niejasno tłumaczę.
Zobrazować (narysować rysunek) mogę Ci to dla talii trójkolorowej (
•,
•,
•).
Załóżmy, że też mamy po 13 kart w kolorze i też wybieramy 6 kart.
Będzie:
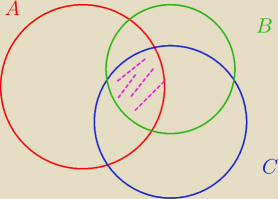
Oznaczenia zbiorów z rysunku:
A // zbiór takich wyborów 6 kart (zbiorów 6−elementowych), że przynajmniej jedna jest w
kolorze
•
B // zbiór takich wyborów 6 kart (zbiorów 6−elementowych), że przynajmniej jedna jest w
kolorze
•
C // zbiór takich wyborów 6 kart (zbiorów 6−elementowych), że przynajmniej jedna jest w
kolorze
•
Chcemy policzyć |A∩B∩C|, znaczy część wspólną tych zbiorów (
fiolet), i liczymy to tak:
|A∩B∩C|=
Dla 4 kolorów analogicznie (tylko ciężej narysować
).
