aa Aleks: Rozwiąż nierówność: 1+log₂(sin2x)+log²₂(sin2x)+...<0,(6) w zbiorze <0,2π>, gdzie lewa strona nierówności jest szeregiem zbieżnym już po tych ogólnych obliczeniach...

	π		π		5
zał. x∊(kπ,		+kπ), k∊C ⋀ x∊(		+kπ,		π+kπ), k∊C
	2		12		12

1		2
	<		/ *3
1−log2(sin2x)		3

3
	−2<0
1−log2(sin2x)

log2(sin2x)2+1
	<0
log2(2sin2x)

log2[2*(sin2x)2]
	<0
log2(2sin2x)

korzystają z wzoru na zmianę podstawy logarytmu log_²sin2x[2*(sin2x)²]<0

	2
z założenia wiadomo, że sin2x∊(0,1), więc podstawa logarytmu		>1, więc znak
	sin2x

nierówności(opuszczając logarytm) się nie zmieni, dalej sin²(2x)*2<1

	1
sin2(2x)<
	2

	√2		√2
−		<sin2x<
	2		2

	π		π
−		+kπ<x<		+kπ
	8		8

	π		π
x∊(−		+kπ,		+kπ)
	8		8

Teraz biorąc to wszystko na oś z zał wychodzi mi

	π		π		13		9
x∊(		,		)∨(		π,		π)
	12		8		12		8

w odpowiedziach jest zaś

	π		π		3		5		13		9		11		17
x∊(		,		)∨(		π,		π)∨(		π,		π)∨(		π,		π)
	12		8		8		12		12		8		8		12

Pomoże mi ktoś wskazać błąd?

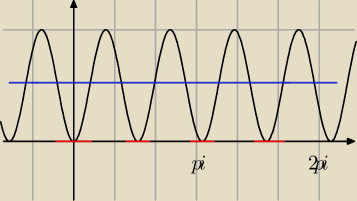aniabb: ano są 4

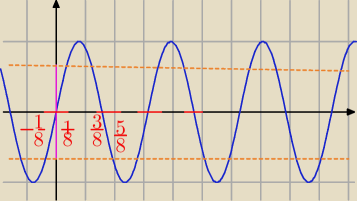aniabb: −π/4<2x<π/4 oraz 3π/4<2x<5π/4

aniabb: to jest od momentu −√2/2<sin2x<√2/2

amm: Bez kitu, chyba juz wczoraj w nocy nie myślałem. Dzięki wielkie