Paramtery Krzysik: Dla jakich m dziedzina funkcji F(X)=√mx²−(1+m)X+1 ma dwa różne rozwiązania dodatnie

PW: Dziedzina jest zbiorem, pytanie jest źle postawione.

Krzysik: Przepraszam powinno być * jest zbiór liczb rzeczywistych

Krzysik: Obliczyłem deltę i wyszło że X1=(1+m+4√2)/2m i X2=(1+m−4√2)/2m

Krzysik: I nie wiem co teraz

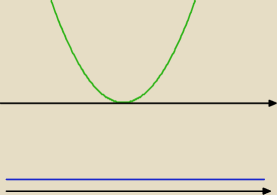
iteRacj@: jeśli dziedziną funkcji F(x) ma być zbiór liczb rzeczywistych: 1/ funkcja podpierwiastkowa g(x)=mx²−(1+m)x+1 jest f.liniową postaci y=ax+b i przyjmuje tylko a/ wartośći dodatnie ⇔ a=0 i b>0 tutaj a=−(1+m) i b=1 lub b/ wartość zero ⇔ a=0 i b=0 2/ funkcja podpierwiastkowa g(x)=mx²−(1+m)x+1 jest f.kwadratową postaci y=ax²+bx+c i przyjmuje tylko ylko a/ wartości nieujemne a≠0 i Δ≤0 tutaj a=m, b=−(1+m), c=1 musisz obliczyć, dla jakich wartości parametru m te warunki są spełnione

iteRacj@: * poprawka do 2/przyjmuje tylko wartości nieujemne a>0 i Δ≤0

Krzysik: A muszę obiczyc założenie że pod pierwiastkiem większe równe zero? Bo wyliczyłem i wyszły mi takie dziwne x jak powyzej

Krzysik: *mój błąd cofam. Ale nie rozumiem czemu w funkcji liniowej jest inne a i b niż w kwadratowej

aniabb: bo nazywają po kolei abc te cyferki co się pojawiają czyli w kwadratowej ax²+bx+c w liniowej ax+b więc jak Ci znika x² to z kwadratowej zostaje bx+c ale we wzorach masz wszędzie ax+b i dlatego