Wyznacz zbiór rozwiązań równania |x+1| + |x−2| = m, w zależności od parametru m. Kamil: Wyznacz zbiór rozwiązań równania |x+1| + |x−2| = m, w zależności od parametru m. Wszystko mam tylko nie wiem jak wyznaczyć zbiór rozwiązań, odpowiedzi mam i nie wiem skąd m jest < 3 dla 0 rozwiązań i czemu m>3 ma rozwiązania. 1. x ∊ (−∞, −1) ⇒ |x + 1| = −x − 1, |x − 2| = −x + 2 − x − 1 − x + 2 = m −2x + 1 = m 2. x ∊ <−1,2) ⇒ |x + 1| = x + 1, |x − 2| = −x + 2 x + 1 − x + 2 = m 3 = m 3. x ∊ <2, ∞) ⇒ |x + 1| = x + 1, |x − 2| = x − 2 x + 1 + x − 2 = m 2x − 1 = m

Janek191: Zrób graficznie

PW: Na pytanie dlaczego dla m<3 jest zero rozwiązań można odpowiedzieć tak: |x+1|+|x−2|=|x+1|+|−x+2|≥|x+1+(−x+2)|=|3|=3 Skoro lewa strona jest większa lub równa 3, to równanie |x+1|+|x−2| = m nie ma rozwiązań dla m<3.

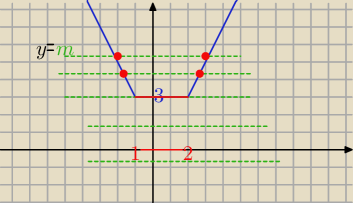
Eta: 1/ dla m >3 2 rozwiązania dla m=3 x∊(1,2) −−− nieskończenie wiele rozwiązań w tym przedziale dla m<3 −− 0 rozwiązań