Stereometria
GOŚĆ: podstawą ostrosłupa ABCS jest równoramienny trójkąt prostokątny ABC o kącie prostym przy
wierzchołku C. Wysokość SE ściany bocznej ABS jest jednocześnie wysokością ostrosłupa. Punkt E
jest środkiem krawędzi AB. Punkt D jest środkiem krawędzi CS. Pole trójkąta ABD jest równe p,
a płaszczyzna, w której leży trójkąt ABD jest nachylona do płaszczyzny podstawy ostrosłupa pod
kątem α. Wyznacz objętość ostrosłupa ABCS w zależności od p oraz α.
25 mar 19:18
Mila:
Masz odpowiedź do zadania?
25 mar 20:44
GOŚĆ: Największy problem jest w tym, że nie mam
25 mar 20:56
Mila:
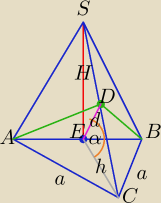
1) ∡C=90
o
2)ΔSEC− Δprostokątny
|DC|=d⇔|SC|=2d
(2d)
2=H
2+h
2⇔
3) W ΔCED:
d
2=d
2+h
2−2*d*hcosα
porównanie z (*)
| a√2 | | 2p | |
| = |
| ⇔ a2=4*p*cosα |
| 4cosα | | a√2 | |
a=2
√p*cosα
| | a√2 | | a√2 | | 1 | | 1 | |
4) (2* |
| )2=H2+( |
| )2 ⇔H2= |
| a2*( |
| −1) |
| | 4cosα | | 2 | | 2 | | cos2α | |
| | 1 | | 1−cos2α | | 1 | |
H2= |
| a2* |
| ⇔H2= |
| a2*tg2α |
| | 2 | | cos2α | | 2 | |
5)
| | 1 | |
V= |
| *4*p*cosα*tgα*2√p*cosα |
| | 6√2 | |
====================
Posprawdzaj rachunki.
25 mar 21:40
Mila:
Może
Eta pojawi się, to może poda swój wynik.

25 mar 21:43

