pochodna Ktoś:

	8
|AP|=√(2−x)2+(−2−		)2
	x

Moglby ktos pokazac jak obliczyc z tego pochodna, wiedzac ze x∊(0,∞)?

Ktoś:

Ktoś:

Eta: Napisz oryginalną treść zadania ..........

Ktoś: Na galezi paraboli o rownaniu y=8/x, gdzie x∊(o,∞), wyznacz taki punkt P, ktorego odleglosc od punktu A(2,−2) jest najmniejsza.

Ktoś:

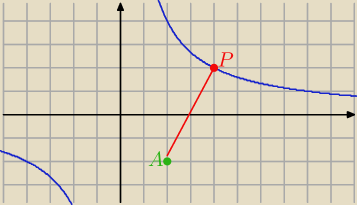
Eta: na gałęzi hiperboli ! ( bo wykresem y=8/x −− jest hiperbola! A(2,−2) , P(x,8/x) i x>0

	8		64		32
|AP|2=(x−2)2+(		+2)2 = x2−4x+4+		+		+4
	x		x2		x

	64		32
|AP|2= x2−4x+8+		+
	x2		x

	64x		32
f'(x) = 2x−4−		*2x−
	x4		x3

f^'(x)=0 2x⁴−4x³−32x−128=0 ⇒ x⁴−2x³−16x−64=0 ⇒ (x²−2x−8)(x²+8)=0 i x>0 ⇒ x=4 i określ czy jest to minimum .............. ....................... Odp: x= 4 to y= 8/4= 2 P(4,2) ======

Eta: Poprawiam zapis

	64		32		128		32
f'(x)= 2x−4−		*2x−		= 2x−4−		−
	x4		x2		x3		x2

Ktoś:

	32		a
nie bardzo rozumiem co sie stalo z		, bo z wzoru na pochodna f(x)=
	x		x

	−a
f'(x)=
	x2

Za to parabole przepraszam, na szybko przepisywalem

Ktoś: ok juz wiem XD

Eta: