zad adam: Dany jest trójkąt ostrokątny ABC. Punkty P i Q są rzutami prostokątnymi odpowiednio punktów A i B na proste BC i AC, a punkty R i S są rzutami prostokątnymi odpowiednio punktów A i B na prostą PQ. Wykaż, że PR=QS.

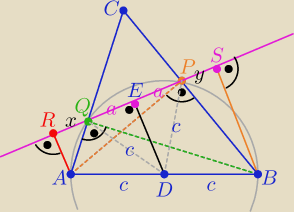
Eta: 1/ przejrzysty rys. zgodnie z treścią zadania 2/ na czworokącie ABPQ można opisać okrąg ( dlaczego? którego średnicą jest AB i D −− jest środkiem tego okręgu 3/ ΔPQD jest równoramienny o ramionach c to E jest środkiem PQ , zatem |QE|=|EP|=a 4/ |RQ|=x , |PS|=y to |RP|=x+2a i |SQ|=y+2a ponieważ AR,DE , BS są równoległe to E jest środkiem RS zatem c=x+2a=y+2a ⇒ x=y to |PR|=|QS| =========== c.n.w

adam: a jak to zrobić z pitagorasów?

Krzysiek: ?

Krzysiek:

aniabb: wg rysunku Ety tylko pitagoras AB²= AQ²+QB² = RA²+x²+(2a+y)²+SB² AB²= AP²+PB² = RA²+(x+2a)² + y²+SB² zatem RA²+x²+(2a+y)²+SB² = RA²+(x+2a)² + y²+SB² x²+4a²+4ay+y²=x²+4ax+4a²+y² 4ax=4ay x=y