Krawędź podstawy ostrosłupa prawidłowego trójkątnego ma długość a xmax: Krawędź podstawy ostrosłupa prawidłowego trójkątnego ma długość a, natomiast cosinus kąta

	7
między jego sąsiednimi ścianami bocznymi jest równy		. Wyznacz objętość tego ostrosłupa.
	15

iteRacj@: czy masz odpowiedź do tego zadania?

xmax:

	√11
V =		a3
	12

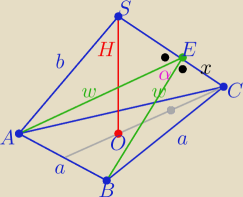
Eta: 1/ z tw. cosinusów w ΔABE

	w2+w2−a2		7
cosα=		=		⇒ ... w2= 15a2/16
	2w2		15

2/ z tw. Pitagorasa w ΔBCE x²= a²−w² ⇒ .... x=a/4 to w ΔAES b²= w²+(b−x)² ⇒ ............ b= 2a 3/ w ΔOSC : |OC|=a√3 i |SC|=2a to H= a

	a3√3
V=
	12

===========

Eta: @xmax Skąd te √11 ?

iteRacj@:

	√3
mnie wychodzi |OC|=a
	3

iteRacj@: i daje to √11

Eta: Racja..... źle podstawiłam za |OC|

Eta:

	√3a
|OC|=
	3

H= √4a²−(a²/3) = U{√11{√3a

	a2√3		√11a		√11a3
V=		*		=
	12		√3		12