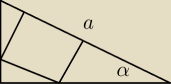
 W trójkąt prostokątny o przeciwprostokątnej a i kącie α, wpisano kwadrat. Oblicz pole tego
kwadratu
W trójkąt prostokątny o przeciwprostokątnej a i kącie α, wpisano kwadrat. Oblicz pole tego
kwadratu
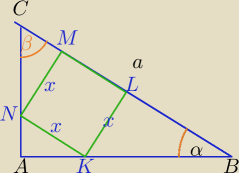 1)
PKLMN=x2
2)
1)
PKLMN=x2
2)
| x | ||
W ΔBLK: tgα= | ⇔|BL|=x*ctgα | |
| |BL| |
| x | x | |||
W ΔCMN: tg(90−α)= | ⇔ctgα= | ⇔|CM|=x*tgα | ||
| |CM| | |CM| |
| a | ||
x= | ||
| tgα+ctgα+1 |
| a2 | ||
PKLMN= | ||
| (tgα+ctgα+1)2 |
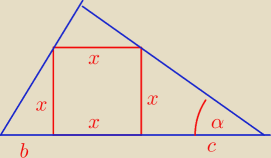 Mamy
Mamy
| x | x | ||
= tg α ⇒ x = c tg α ⇒ c = | |||
| c | tg α |
| x | x | ||
=tg( 90o − α) = ctg α ⇒ x = b ctg α ⇒ b = | |||
| b | ctg α |
| x | x | ||
+ x + | = a | ||
| ctg α | tg α |
| 1 | 1 | |||
x*( | + 1 + | ) = a | ||
| ctg α | tg α |
| a | ||||||||||||||
x = | ||||||||||||||
|
