wykaz
ruzamka: W graniastosłupie prawidłowym trójkątnym przekątna ściany bocznej tworzy z krawędzią boczną kąt
o mierze beta. Miara kąta nachylenia tej przekątnej do sąiedniej ściany bocznej graniastosłupa
| | √3tgbeta | |
jest równa alfa.Wykaż,że tg alfa = |
| j |
| | √4+tg2beta | |
24 mar 19:51
ruzamka: umie ktoś?
24 mar 20:27
iteRacj@: tak, rozwiążę to
24 mar 20:31
Mila:
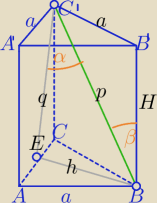
1) W ΔC'B'B:
a=H*tgβ
2)
3)
W ΔC'CE:
| | 1 | | 1 | |
q2=H2+ |
| H2*tg2β=H2*(1+ |
| tg2β) |
| | 4 | | 4 | |
==================
24 mar 20:39
iteRacj@:
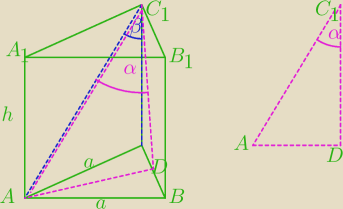
a=h*tg β
| | √3 | | √3 | |
|AD|= |
| *a= |
| *h*tg β |
| | 2 | | 2 | |
|CD|=|DB|
| | a | | h*tg β | | tg β | |
|DC1|2=h2+( |
| )2=h2+( |
| )2=h2[1+( |
| )]2 |
| | 2 | | 2 | | 2 | |
24 mar 20:40
ruzamka: dzieki!
24 mar 21:01
ruzamka: a czemu tgalfa=a/h?
24 mar 21:23
Mila:
U mnie jest inaczej.

24 mar 21:35
ruzamka: @iteRacj@?
24 mar 21:35
ruzamka: Mila,u Cb tez jest a/H
24 mar 21:36
ruzamka: aaa
24 mar 21:36
ruzamka: niee
24 mar 21:36
ruzamka: sorki,jest tam beta
24 mar 21:38
iteRacj@:
β to kąt między przekątną ściany bocznej a krawędzią boczną czyli wysokością graniastosłupa,
tak wynika z tresci
Mila u mnie jest tak samo, tylko na rysunku inaczej zaznaczone
24 mar 21:43
ruzamka: Juz wszystko widze,po prostu wydawało mi się,że tam jest alfa a nie beta
24 mar 21:45
ruzamka: wielkie dzieki <3
24 mar 21:45



 β to kąt między przekątną ściany bocznej a krawędzią boczną czyli wysokością graniastosłupa,
tak wynika z tresci
Mila u mnie jest tak samo, tylko na rysunku inaczej zaznaczone
β to kąt między przekątną ściany bocznej a krawędzią boczną czyli wysokością graniastosłupa,
tak wynika z tresci
Mila u mnie jest tak samo, tylko na rysunku inaczej zaznaczone