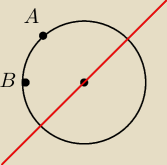
 Srodek okregu przechodzacego przez punkty A=(3,0) i B=(0,1) należy do prostej y=x+2.
Znajdz rownanie tego okregu.
Wiem,że mozna to zrobic za pomoca rownania okregu (x−a)2+(y−b)2=r2 i uklad rownan,ale
ma ktos moze pomysl jak to zrobic inaczej?Myslalem na poczatku,zeby wyznaczyc prostopadla
do prostej AB wstawiajac wspolrzedne srodka AB ale nie wiem czy by to cos dalo..
Srodek okregu przechodzacego przez punkty A=(3,0) i B=(0,1) należy do prostej y=x+2.
Znajdz rownanie tego okregu.
Wiem,że mozna to zrobic za pomoca rownania okregu (x−a)2+(y−b)2=r2 i uklad rownan,ale
ma ktos moze pomysl jak to zrobic inaczej?Myslalem na poczatku,zeby wyznaczyc prostopadla
do prostej AB wstawiajac wspolrzedne srodka AB ale nie wiem czy by to cos dalo..
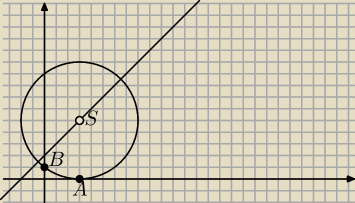 (3−x)2+(0−x−2) = (0−x)2+(1−x−2)2
⇒
współrzędne środka:
x=3
y =x+2 = 5
r2 = 32 +42 = 25
równanie okręgu:
(x−3)2+(y−5)2 = 25
(3−x)2+(0−x−2) = (0−x)2+(1−x−2)2
⇒
współrzędne środka:
x=3
y =x+2 = 5
r2 = 32 +42 = 25
równanie okręgu:
(x−3)2+(y−5)2 = 25
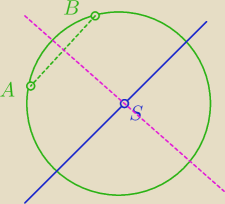 |SA|=|SB|=r a więc punkty A i B są równoodległe od pkt S
zbiór punktów równoodległych od końców odcinka to jego symetralna
znajdź jej równanie
następnie znajdź punkt wspólny symetralnej i prostej y=x+2
to będzie środek okręgu S
|SA|=|SB|=r a więc punkty A i B są równoodległe od pkt S
zbiór punktów równoodległych od końców odcinka to jego symetralna
znajdź jej równanie
następnie znajdź punkt wspólny symetralnej i prostej y=x+2
to będzie środek okręgu S
| yA−yB | ||
a= | ||
| xA−xB |