Trójkąt ostrokątny
Piotrek: Punkt D jest punktem przecięcia się wysokości trójkata ostrokątnego ABC, w którym CD=AB a kąt
ABC ma miarę 70 stopni. Wyznacz miary pozostałych kątów tego trójkąta.
Wykaż, że AB≥√(2−√2)BC ×AC
24 mar 11:46
iteRacj@:
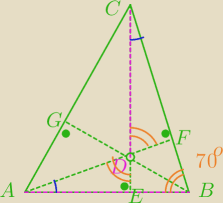
|CD|=|AB|
D − ortocentrum
|<ABC|=70
o
|<BCA|=?, |<CAB|=?
|<ECF|=90
o−70
o=20
o
|<CDF|=|<ADE|=70
o
|<FAB|=90
o−70
o=20
o
stąd ΔAFB≡ΔCDF (kbk)
i |CF|=|AF| oraz |FB|=|FD|
ΔDFB równoramienny
| | 1 | |
|<FDB|=|<FBD|= |
| *(180o−90o)=45o |
| | 2 | |
|<GDA|=|<GAD|=45
o
|<CAB|=|<GAD|+|<DAB|=45
o+20
o=65
o
24 mar 12:49
Piotrek: A jak wykazać że AB≥√(2−√2)BC ×AC
24 mar 15:04
iteRacj@:
skorzystaj z twierdzenia cosinusów, oblicz długość boku AB
24 mar 15:09
 |CD|=|AB|
D − ortocentrum
|<ABC|=70o
|<BCA|=?, |<CAB|=?
|<ECF|=90o−70o=20o
|<CDF|=|<ADE|=70o
|<FAB|=90o−70o=20o
stąd ΔAFB≡ΔCDF (kbk)
i |CF|=|AF| oraz |FB|=|FD|
ΔDFB równoramienny
|CD|=|AB|
D − ortocentrum
|<ABC|=70o
|<BCA|=?, |<CAB|=?
|<ECF|=90o−70o=20o
|<CDF|=|<ADE|=70o
|<FAB|=90o−70o=20o
stąd ΔAFB≡ΔCDF (kbk)
i |CF|=|AF| oraz |FB|=|FD|
ΔDFB równoramienny