czworościan asd: Płaszczyzna równoległa do podstawy czworościanu i przechodząca przez punkt K będący środkiem wysokości czworościanu dzieli go na dwie bryły. Oblicz stosunek objętości otrzymanych brył. Jak wyznaczyć tutaj pole podstawy mniejszej bryły?

asd: * czworościanu foremnego

Tadeusz: a musisz wyznaczać to pole podstawy? ... wyznacz skalę podobienstwa i dalej z górki

asd: pole małej podstawy do dużej ma k=1/4? czy źle myślę?

Tadeusz:

Mila:

	1
ΔKLM∼ΔABC w skali k=
	2

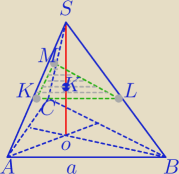
	1
Ostrosłup ABCS∼ostr. KLMS w skali k=
	2

Stosunek objętości brył podobnych jest równy sześcianowi skali podobieństwa ===================================== V− objętość ostr.ABCS

VKLMS		1		1
	=(		)3⇔VKLMS=		V
V		2		8

	1		7
VABCKLM=V−		V=		V
	8		8

Stosunek objętości otrzymanych brył

1   V 8
	= ?
7   V 8