funkcje trygonometryczne anulka__1990:

	2
oblicz wartości pozostałych funkcji trygonometrycznych gdy sinα=
	3

jak to zrobic jak obliczyc brakująca długoś boku w trójkącie wiem ze za pomoca twierdzenia pitagorasa ale nie chce mi wyjsc..

Julek: cosα = √1−sin²α

	sinα
tgα =
	cosα

	1
ctgα = cosαsinα =
	tgα

scorpi:

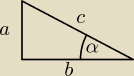
	a
sinα=		, więc a= 2 i c= 3
	c

a² + b² = c² b² = c² − a² b² = 9 − 4 b = √5

	b
cosα =
	c

	√5
cosα =
	3

	a
tgα =
	b

	2		2√5
tgα =		=
	√5		5

	b
ctgα =
	a

	√5
ctgα =
	2

Tomasz:

4		4
	+cos2=1 /:
9		9

	4
1 sprowadzamy do wspólnego mianownika z
	9

	9
czyli:
	9

	9		4		9
więc		:		=
	9		9		4

	9
cos=√
	4

	1
cos=√2		=√2,25
	4

cos=√2,25 cos=1,5 Resztę koleżanko można zrobić zaglądając na tej stronie na "trygonometria" i "Związki pomiędzy funkcjami trygonometrycznymi" nie jest to trudne

Tomasz: sorry pomyliłem zadanie to odpowiedź dla kogoś innego

anulka__1990: dziekuje