 Pewna metoda izotopowa wykrywania uszkodzeń daje następujące
wyniki: jeśli urządzenie ma uszkodzenie to metoda ta pozwala
na jego wykrycie w 90% przypadków i nie wykrywa go w
10% przypadków, jeśli urządzenie nie ma uszkodzenia to metoda ta daje w
99% przypadków informacje zgodne ze stanem faktycznym
i w 1% przypadków informuje o defekcie, którego nie ma.
W pewnej partii urządzeń jest 2%, mających defekt. Jakie
jest prawdopodobieństwo, że wybrane losowo urządzenie ,
rozpoznane jako uszkodzone jest rzeczywiście uszkodzone?
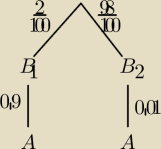
B1 urządzienie uszkodzone
B2 urządzenie nieuszkodzone
A wykrycie uszkodzenia
Pewna metoda izotopowa wykrywania uszkodzeń daje następujące
wyniki: jeśli urządzenie ma uszkodzenie to metoda ta pozwala
na jego wykrycie w 90% przypadków i nie wykrywa go w
10% przypadków, jeśli urządzenie nie ma uszkodzenia to metoda ta daje w
99% przypadków informacje zgodne ze stanem faktycznym
i w 1% przypadków informuje o defekcie, którego nie ma.
W pewnej partii urządzeń jest 2%, mających defekt. Jakie
jest prawdopodobieństwo, że wybrane losowo urządzenie ,
rozpoznane jako uszkodzone jest rzeczywiście uszkodzone?
B1 urządzienie uszkodzone
B2 urządzenie nieuszkodzone
A wykrycie uszkodzenia
| P(A|B1)*P(B1) | ||
P(B1|A)= | ||
| P(A) |
| 2 | 98 | 278 | ||||
P(A)= 0,9* | + 0,01* | = | ||||
| 100 | 100 | 10000 |
| 180 | ||
P(A|B1)= | ||
| 10000 |
| 2 | ||
P(B1)= | ||
| 100 |
| 180 | ||
P(B1|A)=.. no właśnie.. powinienem otrzymać | czyli jakby iloczyn P(A|B1) i P(A), | |
| 278 |
| P(A∩B1) | ||
P(B1|A) = | ||
| P(A) |
| 0,02*0,9 | 0,0180 | |||
P(B1|A) = | = | |||
| 0,02*0,9+0,01*0,98 | 0,0278 |