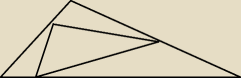
Pola trójkątów Narina: Punkty K, L oraz M leżą odpowiednio na bokach AB, BC, AC w taki sposób że AK/BK=1/2 CM/AM=3/4 BL/CL=2/3. Pole trójkąta KLM jest równe 6. Oblicz pole trójkąta ABC

Eta: P(ABC)=21

Mila: P=P_ΔABC 1)

	1		1
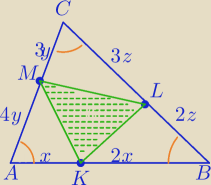
P=		*3x*7y*sin∠A i PΔAKM=		x*4y*sin∠A
	2		2

PΔAKM		1   x*4y*sin∠A 2
	=
P		1   *3x*7y*sin∠A 2

	4
PΔAKM=		P
	21

============= 2)

	1
PΔKBL=		*2x*2z*sin∠B
	2

PΔKBL		1   *2x*2z*sin∠B 2
	=
P		1   *3x*5z*sinB 2

	4
PΔKBL=		P
	15

================ 3)

	1
PΔLMC=		*3z*3y*sinC
	2

PΔLMC		1   *3z*3y*sinC 2
	=
P		1   *5z*7y*sinC 2

	9
PΔLMC=		P
	35

============== 4) Suma pól:

4		4		9
	P+		P+		P+6=P
21		15		35

5
	P+6=P
7

2
	P=6
7

P_ΔABC=21 ===========