Oblicz pole przekroju i sinus kąta nachylenia płaszczyzny tnącej do podstawy dol Hala: W sześcianie o krawędzi 8 cm poprowadzono płaszczyznę tnącą przez przekątną dolnej podstawy i środek krawędzi górnej podstawy. Oblicz pole przekroju i sinus kąta nachylenia płaszczyzny tnącej do podstawy dolnej sześcianu.

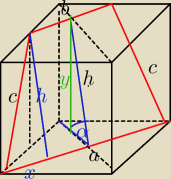
Basia: Przekrój to trapez równoramienny a² = 8²+8² = 2*8² a = 8√2 b² = 4²+4² = 2*4² b = 4√2 c² = 4²+8² = 16+64 = 80 = 16*5 c = 4√5

	a−b		8√2−4√2
x=		=		= 2√2
	2		2

x²+h²=c² h² = c²−x² = 80−8 = 72 = 36*2 h = 6√2

	a+b
P =		*h = ..................................
	2

podstaw i policz

	a
y2+ (		)2 = h2
	4

y² = 72−8 = 64 y=8

	y
sin α =		= ..........................................
	h

podstaw i dokończ obliczenia