graniastosłupy Stanisław: Podstawą graniastosłupa prostego jest trapez o podstawach długości 2 i 9 oraz ramionach 5 i 4√2. Wiedząc, że obj tego graniastosłupa wynosi 220 oblicz długości przekątnych graniastosłupa. Proszę o pomoc Ma wyjść √152 i √134

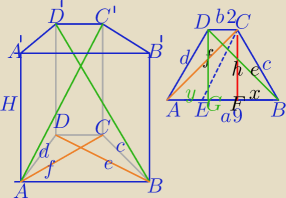
Mila: c=5, d=4√2 1) CE||AD |EB|=7 P_ΔEBC z wzoru Herona

	5+7+4√2
p=		=6+2√2
	2

P_Δ=√(6+2√2)*(6+2√2−4√2)*(6+2√2−5)*(6+2√2−7)= =√(6+2√2)*(6−2√2)*(1+2√2)*((2√2−1)= =√(36−8)*(8−1)=√28*7=√196=14

	1
PΔ=14=		*7*h⇔h=4 wysokość trapezu
	2

2) Pole trapezu:

	9+2
PABCD=		*4=22
	2

V=220=22*H⇔ H=10 3)W ΔCFB c²=x²+h²⇔5²=x²+4² x=3 4) Przekątna AC: W ΔAFC: |AF|=9−3=6 f²=6²+4²=36+16=52 5) Przekątna graniastosłupa BD' |AC'|²=H²+f² |AC'|²=10²+52²=152 |AC'|=√152 ============== 5) przekątna trapezu BD y²=(4√2)²−4²=16, y=4 W ΔGBD: |DB|²=5²+4²=41 6) Przekątna gran. BD' |BD'|²=|DB|²+H²=41+100=141 |BD'|=√141 ========== sprawdzaj rachunki

Stanisław: Dziękuję

Mila: druga przekątna nie zgadza się, sprawdzaj.