funkcja kwadratowa-równania Michał: Dobry wieczór! To znowu ja z tymi samymi problemami Próbuję rozwiązać równanie √x−1=x−3 wpadłem na błyskotliwy pomysł podnieś do kwadratu wiec chyba dwa założenia x−1>=0 dla x−1=x²−6x+9 x−1<0 dla −x+1=x²−6x+9 Dobrze myślę? I teraz tak; x>=1 0=x²−7x+10 Δ=49−40=9 x₁=2 x₂=5 oba są w przedziale oba x to odp. x<1 −x+1=x²−6x+9 Δ=25−32<0 BRAK m.z czyli zostaje x=5 i x=2 tylko ze przy podstawieniu do wzorku 5 i 2 tylko 5 się zgadza wychodzi równość. Hmnn moje pytanie, mam jakiś błąd że mi wyszła ta 2? Dobry sposób obrałem? Zawsze mam na końcu robić to sprawdzenie? A moze pominąłem jakiś zakres?

Mila: √x−1=x−3 D_r: x−1≥0 i x−3≥0⇔x≥3 Podnosimy obustronnie do kwadratu x−1=x²−6x+9⇔ x²−7x+10=0 Δ=49−40=9

	7−3
x=		=2∉D lub x=5∊D
	2

odp. x=5

Michał: Dziękuję Mila, czyli wnisoek dla mnie: gdy mam niewiadome w równaniu po obu stronach, i po jednej mam wartość bezwględną >=0 to dla drugiej strony równania też wynik musi być >=0 ? Dobrze rozumiem? I cześć wspólna tych nierówności to moja dziedzina?

Saizou : Michał mogłeś tak zrobić, ale na końcu sprawdzić wyniki, czy spełniają one równanie wyjściowe. To się nazywa metoda analizy starożytnych i "pojawia" się ona w nowej podstawie programowej.

Mila: Mogłeś zrobić bez założeń, ale wyniki należy sprawdzić. Ja dałam założenie, że wyrażenie pod pierwiastkiem nieujemne, ale wtedy prawa strona też ≥0 ( wynik pierwiastkowania dodatni lub 0)

Michał: Aaaa ok, to drugie założenie, meh x−3>=0 hmmm muszę o tym pamiętać jak by co, dzięki bardzo za pomoc!

Mila:

Michał: Ok, mam inny przykład zastanawiam się jaka tu by była dziedzina x−2√x−2=6 zrobiłem tak: −2√x−2=6−x |² no to chyba 6−x>=0 ⇔ x<=6 a to drugie to chyba tak x−2>=0 ? x>=2? Z czego potem mnożę to *−2 czyli wynik <=0 więc 6−x<=0 chyba tak powinno być x>=6 czyli D∊<6;+oo)? No w kazdym razie mamy tak 4(x−2)=36−12x+x² x²−16x+44=0 Δ=80 x₁=8−2√5 x₂=8+2√5 odp prawidłowa to 8+2√5 czyli by się zgadzało, dobrze rozumiem? #skomplikowane te dziedziny Tutaj ta metoda starożytnych chyba ciężko by było :X

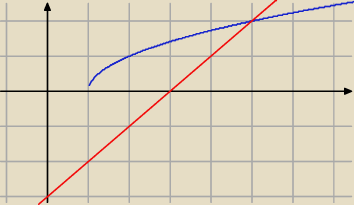
PW: O pierwszym zadaniu. Błyskotliwy byłby pomysł najprostszy: − dla x=5 równanie jest spełnione (to widzi przeciętny gimnazjalista), − innych rozwiązań nie ma, bo (co widzi przeciętny licealista?).

Michał: Bo wykresy mają jeden punkt wspólny, oba równanie √x−1 i x−3 przyjmuja dla kazdej wartosci tylko 1 rozwiązanie.

Michał: O ile dobrze rozumiem :X

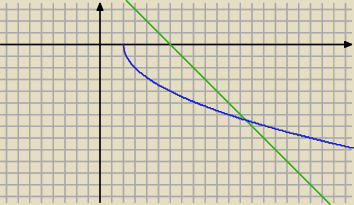
Michał: I tak samo w drugim przykładzie, ale jezeli sobie tego wykresu nie narysuje, nie jestem w stanie stwierdzić, która odp. jest prawidłowa(chyba), a z tymi wykresami, bez komputra, może być ciężko. Choćby w drugim przykładzie, o który pytam (19:33).

Mila: x−2√x−2=6⇔ x−6=2√x−2 D_r: x−2≥0 i x−6≥0⇔x≥6 x²−12x+36=4*(x−2) x²−16x+44=0 itd

Michał: Mmmm, dziękuję Mila jesteś wielka (MEGA bardzo Ci dziękuję)... Tylko, gdzie ja zrobiłem błąd, bo chyba dobrze operuje tymi liczbami

PW: Drugie zadanie: x−2√x−2=6, odejmujemy stronami liczbę 2: (x−2)−2√x−2=4 Podstawiamy √x−2=t≥0 (z uwagi na dziedzinę pierwiastka) t²−2t=4 t²−2t−4=0 Δ=20, √Δ=2√5 Nieujemne rozwiązanie to t=1+√5, czyli √x−2=1+√5 x−2=6+2√5 x=8+2√5. Nic specjalnie mądrego nie zrobiłem, ale wydaje się że odjęcie dwójki stronami na samym początku uprościło rachunki (nie trzeba było podnosić obu stron do kwadratu).

Michał: No, być może ale jak dla mnie mega to sprytne PW, eh ja jestem za głupi na takie pomysły, nie wiem jakoś nie widzę tego. Ale bardzo dziękuję Ci za pokazanie mi tego rozwiązania i takie rozpisanie =) Bo jest to dla mnie mega intrygujące, że tym sposobem to wyszło .