udowodnij że długość odcinka dwusiecznej kąta prostego w trójkącie prostokątnym alinka: udowodnij że długość odcinka dwusiecznej kąta prostego w trójkącie prostokątnym o przyprostokątnym dł a i b zawartego między wierzchołkiem kąta i przeciwprostokatna jest równa

	ab√2
	a+b

Mila:

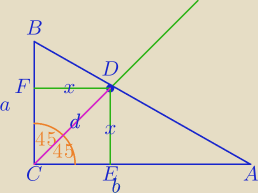
	BF		a
1) ΔDFB∼ΔACB⇔		=		⇔
	x		b

a−x		a
	=
x		b

⇔b*(a−x)=x*a a*b−b*x=x*a a*b=a*x+b*x x*(a+b)=a*b

	a*b
x=		− długość boku kwadratu
	a+b

	ab√2
d=
	a+b

============

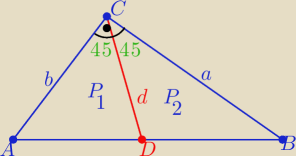Eta: 2 sposób

	ab		bd		bd√2		ad√2
P(ABC)=		, P1=		*sin45o =		P2=.. =
	2		2		4		4

	2ab
bd√2+ad√2= 2ab ⇒ d√2(a+b)=2ab ⇒ d=
	√2(a+b)

	√2ab
d=
	a+b

=========

Mila: III sposób równoważność pól

1		1		1
	a*b=		*x*(b−x)+		x*(a−x)+x2
2		2		2

1		1		1		1		1
	a*b=		bx−		x2+		a*x−		x2+x2
2		2		2		2		2

1		1		1
	*a*b=		b*x+		a*x
2		2		2

a*b=x*(a+b)

	a*b
x=
	a+b

	ab √2
d=
	a+b

============

Mila: Dobranoc