wielomaiany parametr Adam68: Dla jakich wartości parametru m równanie x⁴−2mx²−m²+4=0 ma trzy różne rozwiązania? No to robię: x²=t, t≥0 t²−2mt−m²+4=0 Warunki: 1. Δ>0 2. t1>0 3. t2=0 No i problem polega na tym, że nie wiem co zrobić z 2. i 3. warunkiem.

aniabb: zamień na t₁•t₂=0 t₁+t₂≥0

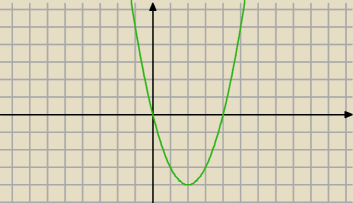
Jerzy: Musisz mieć taką sytuację, a więc jakie warunki ?

Jerzy: Ja bym położył: 1) Δ > 0 2) x_w > 0 3) f(0) = 0

Adam68: Ok, dzięki. A wracając do tego co napisała aniabb − suma t₁+t₂ nie powinna być czasem większa od zera?

aniabb: tak większa

PW: (1) f(x)=x⁴−2mx²−m²+4 jest funkcją parzystą, f(−x)=f(x) dla wszystkich x∊R. Wynika stąd, że jeżeli f(x₁)=0, to również f(−x₁)=0. Wielomian ten może mieć zatem: − dwa miejsca zerowe różne od zera, będące liczbami przeciwnymi − cztery miejsca zerowe różne od zera:: x₁, −x₁, x₂, −x₂ − trzy miejsca zerowe: −x₁, 0, x₁, przy czym 0 jest podwójnym pierwiastkiem wielomianu (1). Istnienie trzech rozwiązań równania oznacza, że mamy do czynienia z trzecią możliwością: f(x)=(x−x₁)(x+x₁)x², f(x)=(x²−x₁²)x². Współczynnik −m²+4 we wzorze (1) musi być więc równy 0: m=−2 lub m=2. Dla takich m jest f(x)=x⁴−2(−2)x² lub f(x)=x⁴−2^.2x² f(x)=x²(x²+4) lub f(x)=x²(x²−4). Jak widać tylko funkcja określona dla m=2 wzorem f(x)=x²(x²−4) spełnia warunki zadania − równanie (1) ma trzy rozwiązania.