Funkcje Jacobss: Wyznacz wzor funkcji liniowej ktora spelnia warunki f(3)=−2 i f(6)=0

Jerzy: f(x) = ax + b −2 = a*3 + b 0 = a*6 + b i oblicz: a i b.

Wika:

Jolanta: f(3)=−2. To znaczy dla x=3 y =−2 Podstawiamy do wzoru y =ax+b −2=3a+b. Tak samo robimy z drugim punktem 0=6a+b. Mamy układ równań ,który możemy rozwiązać metoda podstawiania lub przeciwnych wspolczynnikow

Jolanta: −2=3a+b 0=6a+b. Mnoze pierwsze równanie przez −1 2=−3a−b 0=6a+b. Dodaje w pionie −−−−−−−−−−−−−−− 2=3a / :3 2/3=a Teraz trzeba podstawić za a do pierwszego lub drugiego równania 2/3 i wyliczyć b 2=−3(2/3)+b 2=−2+b 4=b y=2/3x+4

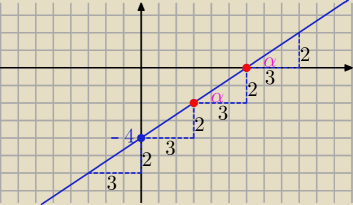
Arabica: Metodą "schodkową"

	y		2
tgα= a=		=		i b= −4
	x		3

y=ax+b

	2
y=		x−4
	3

=========