Geomteria analityczna Ukośnik: Wyznacz równanie prostej prostopadłej do prostej AB i oddalonej od początku układu współrzędnych o √2 A(1,4) B(−6;3). Nie rozumiem, dlaczego wynik wychodzi zły po podstawieniu punktów (−√2;0) i (√2;0) pod równanie prostopadłej :s

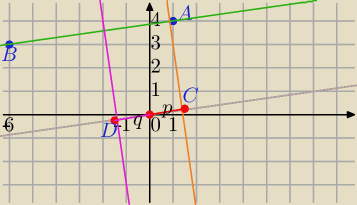
Mila: Prosta AB: 4=a+b 3=−6a+b

	1
a=
	7

b=3⁶₇

	1		27
y=		x+		/*7
	7		7

7y=x+27 x−7y +27=0 Prostopadła do AB p: 7x+y+D=0

	|7*0+1*0+D|
d((0,0),s)=√2=
	√72+12

|D|
	=√2
√50

|D|=√100=10 D=10 lub D=−10 Proste: 7x+y+10=0 lub 7x+y−10=0 p₁: y=−7x−10 lub p₂: y=−7x+10 ==============

	1
y=		x
	7

Odcinki p i q maja długość √2

Ukośnik: A dlaczego mój sposób był zły?

Mila: Nie wiem jaki jest Twój sposób.

Eta: To jeszcze tak k⊥AB

	3−4		1
aAB=		=		to ak=−7
	−6−1		7

k: y= −7x+b ⇒ −7x−y+b=0 i odległa od (0,0) o √2

	|b|
d=		=√2 ⇒ |b|=10 ⇒ b=10 v b= −10
	√50

k: y= −7x+10 lub y= −7x−10 ========================