geometria analityczna lmn: W trójkącie prostokątnym ABC przy wierzchołku B 90. dwa wierzchołki maja współrzędne A(4; −5) C(−8; 5) wyznacz współrzędne wierzchołka B wiedząc że pole wynosi 61. Pomoże ktoś? Obliczyłam wysokość z wierzchołka B i coś z tym próbowałam, ale nie wychodzi, bo nie mam z kolei punktu należącego do tej prostej i prostej AB.

Tadeusz: Zacznij od rysunku Znasz podstawę trójkąta ... znasz pole ... znasz wysokość. Wusokość równa promieniowi ... zatem dwie możliwości ...

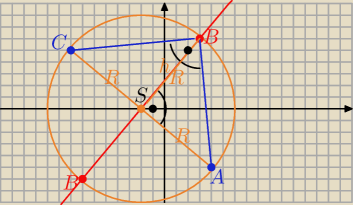
Eta: P=61 , A(4,−5) , C(−8,5) to środek odcina AC : S(−2,0) −−− środek okręgu opisanego na trójkącie prostokątnym ACB

	1
|AC|=2√61 to		*|AC|*h=61 ⇒ h=√61
	2

BS=h= R=√61 i BS ⊥AC zatem trójkąt ABC jest prostokątny i równoramienny zatem jego wysokość zawiera się w symetralnej AC współczynniki kierunkowe :

	5+5		−5		6
aAC=		=		to aBS=
	−8−4		6		5

	6		6
prosta BS: y=		(x+2) zatem B(x,		x+2)
	5		5

|BS|²=R²= 61

	36
(x+2)2+		(x+2)2=61
	25

	61
		(x+2)2=61 ⇒ (x+2)2=25 ⇒ x+2=5 v x+2= −5
	25

x=3 v x= −7 to y= 6 v y= −6 B(3,6) lub B(−7,−6) ===================== I wszystko się zgadza ( na rys.