zadanie QWERTY: Wyrażenie (a+2)² jest od wyrażenia (a+4)²+a²−8: A. 2 razy większe B. 2 razy mniejsze C. o 4 większe D. o 8 mniejsze

Tadeusz: a²+4a+4 2a²+8a+8 2(a²+4a+4)

QWERTY: a to Parabolę o równaniu y=−x² przesunięto o 2 jednostki w kierunku zwrotu osi OX, otrzymując parabolę o równaniu: A. y = −x² – 2 B. y = −(x – 2)² C. y = −(x + 2)² D. y = −x² + 2

QWERTY: zrobiłem to tak ze narysowałem przesunąłem o 2 w prawo później wyznaczyłem wzór funkcji w postaci kanonicznej ale na pewno da się szybciej

the foxi: Tak Przesuwając wykres funkcji f(x) o wektor u=[p;q] otrzymujemy funkcję daną wzorem g(x)=f(x−p)+q, więc Nasz wektor u=[2;0] g(x)=f(x−2)=−(x−2)²

QWERTY: A to https://prnt.sc/iug97t

QWERTY: Napisz równanie symetralnej odcinka o końcach A=(−2;−3),B=(−4;−5).

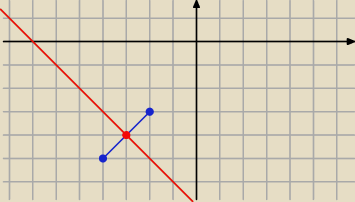XyZ: y= −x−7