Dany jest trójkąt o bokach: 5,5,8 Mati: Dany jest trójkąt o bokach 5,5,8: a) sprawdź jaki jest to trójkąt b) oblicz promień koła wpisanego i opisanego na tym trójkącie c) wyznacz wysokosci tego trójkąta

Tadeusz: pobaw się twierdzeniami sinusów i cosinusów

Mati: Nie przerabialismy jeszcze tego ;<

Mati: Wczesniej mielismy inny trojkat jako przyklad o bokach 61,61,22 z ta sama trescia zadania. Wyszedł trójkąt ostrokątny, a w podpunkcie b) mam takie obliczenia: h²= 61²−11² h²=3600 h=60, z tw Pitagorasa wynika: 11²+ x² R²= 11²+ (60−R)² R²=121+3600−120R+R² 120R=3721 więc b) tutaj mam do połowy, a ostatniego nie mam w ogóle...

Tadeusz: a Pitagoraska już poznałes?

aniabb: ale podali wam regułkę a²+b² <c² rozwartokatny a²+b² > c² ostrokątny a²+b² = c² prostokątny

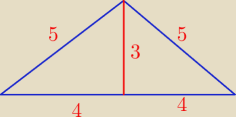
Janek191: P = 4*3 = 12 j² L = 2*5 + 8 = 18 P = 0,5 r*L 2P = r*l

	4
r = 2 P : L = 24 : 18 =
	3

oraz

	a*b*c
P =		⇒
	4 R

	a*b*c		8*5*5		200		25
R =		=		=		=
	$ P		48		48		6

Mati: podpunkt a) mam zrobiony, mam problem z małym obliczeniem małego r, a z wysokoscią myslę, że dam rade. Spróbuję zrozumieć teraz rozwiązanie Janka

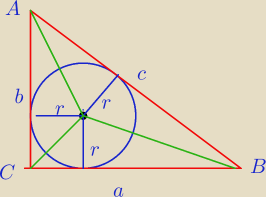
Janek191: P = 0,5 a*r + 0,5 b*r + 0,5 c*r = 0,5 r*(a + b + c) = 0,5 r*L 2 P = r*L

	2 P
r =
	L