LOGARYTMY C.D. bluee:

	1
Wykaż, że jeżeli a,b∊R+ i log4a+log4b+		=log4(a2+b2).
	2

Czy znajdą tutaj zastosowanie wzory skróconego mnożenia ?

bluee:

	ab		1
Jak na razie to mam log4		=−
	a2+b2		2

Jerzy: Jak na razie, to nie ma treści zadania.

bluee: Sorry, ucieło to a=b.

bluee:

	1
Wykaż, że jeżeli a,b∊R+ i log4a+log4b+		=log4(a2+b2), to a=b.
	2

Jerzy: log₄a + log₄b + log₄2 = log₄(a² + b²) ⇔ log₄(a*b*2) = log₄(a² + b²) ⇔ 2ab = a² + b² ⇔ a² − 2ab + b² = 0 ⇔ ( a − b)² = 0 ⇔ a − b = 0

Jerzy: To samo możesz wykazać z równania 13:27 ( wymnóż na krzyż )

aniabb: zamień 1/2 na log₄2 masz 2ab=a²+b² więc a²−2ab+b²=0 (a−b)²=0 to a=b

Jerzy: A nie ... 13:27 to zły trop.

bluee: No tak,ale to będzie log₄1ab=log₄(a²+b²) Jak przeniosę na lewą stronę to będę miała minus czyli wyjdzie mi podzielenie

bluee:

	2ab
log4		=0
	a2+b2

aniabb: czemu

ab		1
	=		to 2ab = a2+b2
a2+b2		2

aniabb: 0=log₄1

aniabb: i nadal 2ab = a²+b²

bluee:

	1
Ale to logarytm z tego ułamka wynosi −		. To skąd mam wiedzieć, że wartość z samego
	2

	1
ułamka wynosie		?
	2

Jerzy: Nie tak..

	2ab		2ab
log4		= 0 ⇔		= 1 ⇔ a2 + b2 = 2ab ⇔ (a−b)2 = 0
	a2+b2		a2+b2

bluee: log₄ x =0 x=1

bluee: Teraz, już rozumiem. Dzięki

Jerzy: 13:43 masz dobrze ... i patrz wyżej.

aniabb: log₄ cokolwiek = −1/2 więc cokolwiek = 4^−1/2 = 1/√4 = 1/2

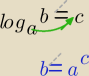
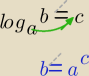aniabb: przenosisz podstawę logarytmu i staje się podstawą potęgi taka mnemotechnika wygodna przy nierównościach jak trzeba pilnować kierunku nierówności (te szare ..gdy a>1 to się nie zmienia)