Hej Nie Radny: Funkcja liniowa przyjmujewartosc dodatnia dla x należących do przedziału od minus nieskończoności do 2 a jej wykres przecina oś OY w punkcie (0,4) zatem jej wzór ma postać. Proszę o wytłumaczenie tego

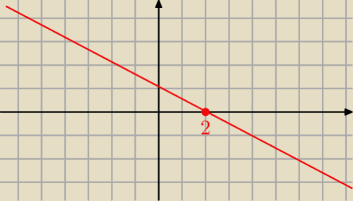
heheszek: hej! to zadanie nie jest trudne. Musisz jednakze miec jakas wiedze. funkcja liniowa skoro ma wartosc dodatnia dla x ∊ (−∞;2> to znaczy ze przecina os X w punkcie (0,2) patrz rysunek.

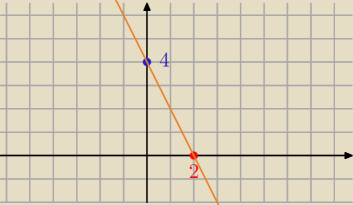
heheszek: wiemy jednakze jeszcze ze przecna os OY w punkcie (0,4) zatem dikladnie tak wyglada ten wykres.

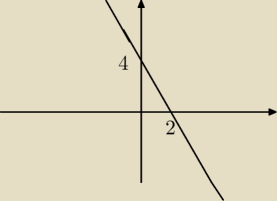
QWERTY: y=ax+b b=4 gdyż jest to punkt przecięcia OY Skoro wiemy że funkcja jest dodatnia od (−∞,2) i że przecina (0,4) to podstawiamy 0=2a+4 a=−2 y=−2x+4

Nie Radny: Czyli wzór wyglada tak ? : y=2x+4 ?

Nie Radny: Spóźniony przepraszam ;−; dziękuje za udzielenie odpowiedzi wszystkim miłej nocy życzę

heheszek: (ocywiscie rysunek nie jest konieczny do wyznaczenia prostej) ale daje jakis poglad jak to wyglada. otoz korzystamy ze wzroru na prosta y = ax+b i podstawiamy te 2 punkty ktore znamy (0,4) oraz (2,0) <−− przeciecie osi OX zatem za igrek daje wspolrzedna igrekowa, za iks wspolrzedna iksowa 0 = a*2+b 4 = a*0+b i rozwiazujemy te rownanie drugie rownanie daje nam od razu 'b' poniewaz 4 = b i wstawiamy to do pierwszego rownania 0 = 2a + 4 −−> 2a = − 4 −−> a = − 2 i wzor koncowy y = −2x + 4 inny sposob to skorzystanie ze wzoru takiego, ze

	YB−YA
a =
	XB−XA

i wtedy wzor funkcji y = a(x−x₀) + y₀ gdzie x₀, y₀ to wspolrzedne punktu albo A albo B dowolny z nich mozna podstawic. wtedy rozw. tego zadania − znowu na punktach (0,4) oraz (2,0)

	0−4		−4
a =		=		= − 2
	2−0		2

zatem y = −2(x−0) + 4 = −2x + 4 jak widac wynik mamy ten sam.

Nie Radny: Dziękuje bardzo za pomoc