parametr- funkcja kwadratowa Michał: Dobry wieczór! Tym razem zadanko z parametrem: Dla jakich wartości parametru m funkcja f przyjmuje tylko wartości ujemne?

	m
f(x)= (m2−1)x2+(m−1)x−
	4

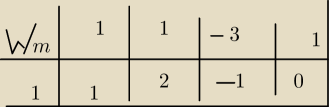
to tak a<0 i Δ<0 czyli: 1. m²−1<0 m²<1 m<1 v m>−1 2. (m−1)²+m(m²−1)<0 m²−2m+1+m³−m<0 m³+m²−3m+1<0 //HORNER −−−> patrz rysunek (m−1)(m²+2m−1)<0 (m−1)(m+1+√2)(m−1−√2)<0 //wykres we wszystkich m.z przejdzie przez ośke X i zaczynamy z góry rysować Dalej już nie piszę że wyznaczam część wspólną bo odp. się nie zgadza. Co chyba oznacza że gdzieś mam błąd w obliczeniach, podejrzewam drugiego punktu. Nie mogę niestety nic wyczaić, może ktoś będzie miał oko i znajdzie luke, dzięki z góry za pomoc pozdrawiam cieplutko. PS. prawidłowa odp to m∊(√2−1;1)

Blee: m=1 także jest odpowiedzią, bo wtedy:

	1		1
f(x) = 0x2 + 0x −		= −		(funkcja stała)
	4		4

druga sprawa: m²+2m−1 = (m + (1+√2))*(m +(1−√2))

piotr: m³+m²−3 m+1<0 ⇒ m<−√2−1 ∨ √2−1<m<1 m²−1 < 0 ⇒ −1<m<1

Michał: No i super teraz wszystko wyszło, dziękuje Blee za ponowną pomoc i Tobie Piotrze. BArdzo doceniam. Meh, ciągle te beznadziejne błędy w przepisywaniu wzorów PS. blee źle chyba wyliczyłeś m²+2m−1 Δ=4+4=8 √Δ=2√2

	−2+2√2
M1=
	2

	−2−2√2
M2=
	2

Blee: (m+1) = 0 −> m = −1 (pierwiastek) analogicznie: m +(1−√2) = 0 −> m = √2 − 1 (pierwiastek) Na dobrą sprawę to ja nie liczyłem pierwiastków tylko wyznaczałem je z pamięci posiłkując się wzorami Viete'a więc: √2−1 + (−√2 − 1) = − 2 −> stąd b=2 (√2−1)(−√2−1) = −2 + 1 = −1 −> stąd c = −1

Blee: fakt ... mogłem zapisać (m − (−√2 − 1))(m − (√2 − 1))

Michał: Ah ok wow, robi wrażenie, nigdy takich cudów nie czynię jak coś liczę, chyba za wysokie loty Podziwiam i masz rację eh . Dzięki raz jeszcze za pomoc.