paramtr m, funkcja kwadratowa Michał: Hello, mam pytanko odnośnie szkicowania wykresów. Należy podać liczbę rozwiązań równania f(x)=|m| w zależności od parametru m. f(x)=|(x+3)²−4| Machłem wykres mam: m=2 ∊ {0} u {1; +oo} m=3 ∊ {1} m=4 ∊ (0;1) W odp jest też powiedziane ze m ma 2 rozzwiązania dla (−oo;−4) U{0}U {4;+oo) i anlogicznie każda odpowiedź ma też wartości na minusie. Zastanawiam się czemu czy to dla tego że: "Należy podać liczbę rozwiązań równania f(x)=|m|"? czyli |m| = 1 to m=1 i m=−1? Potrzebuję potwierdzenia, dziękuję z góry za rozpatrzenie pytania

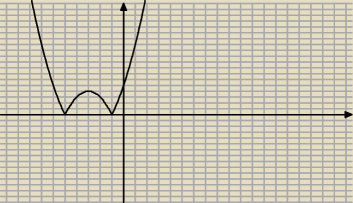
Michał: Hmnn rysunek się coś schrzanił, poprawiam.

PW: |(x+3)²−4|=|m| − jest to równanie typu |a|=|b|, które ma dwa rozwiązania: a=b lub −a=b. Nie zatem "machłem wykres", ale "machłem dwa wykresy".

Michał: Ok, dzięki za zainteresowanie PW =) i wytłumaczenie.