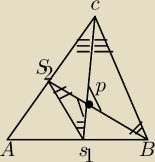
Dowód o srodkowych trójkąta. wifik: Mam wykazać wszystkie 3 srodkowe tylko nie wiem jak to zrobić. Częsć zrobilismy na lekcji, a reszte srodkowych mamy wykazać sami. Z lekcji jest cos takiego: S1S2 równoległe do BC i S1S2=1/2 BC Trójkąt S1S2P jest podobny do trójkąta BPC (kk) w skali k=1/2 S2P=1/2 PB S1P=1/2 PC CND W jaki sposób mam to dokończyć wzorując się tym? Co w tym momencie dowiodłem i jak mam zrobić resztę zadania? Z góry dziękuję

PW: Przepraszam, ale Twoja wypowiedź jest niezrozumiała. Co to znaczy "wykazać środkowe"? Te rozważania mają wykazać jakąś tezę? To chciałbym ją widzieć, bo tak jak sam piszesz − nie wiadomo "co w tym momencie dowiodłem".

wifik: Przepraszam, pomylilem sie. Chodzi o dowiedzenie, ze srodkowe przecinaja sie w jednym punkcie w stosunku 1:2

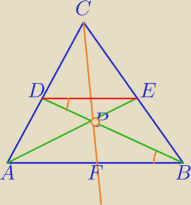
Mila: Twierdzenie Środkowe trójkąta przecinają się w jednym punkcie. Dzieli on każdą z nich w stosunku 2:1 licząc od wierzchołka. 1) Dwie środkowe AE i BD przecinają się w punkcie P.

	1
DE||AB i |DE|=		|AB| z tw. Talesa
	2

	1
ΔDEP∼ΔABP⇔|PD|=		|BP|⇔|BP|=2|PD|
	2

|AP|=2|PE| 2) ABED jest trapezem, wykażemy, że półprosta przechodząca przez punkt przecięcia przekątnych trapezu i punkt C ( przedłużenie ramion ) przechodzi przez środki AB i DE. Za chwilę, po kolacji dokończę, tymczasem analizuj i może sam spróbujesz?

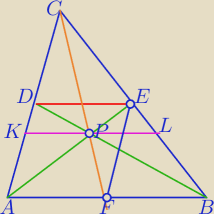
Mila: 1) KL||AB |KP|=|PL|

	KP		PC
ΔKPC∼ΔAFC⇔		=
	AF		CF

	PL		PC
ΔCPL∼ΔCFB ⇔		=		⇔
	FB		CF

KP		PL
	=		⇔|AF|=|FB|⇔
AF		FB

CF przechodzi przez punkt przecięcia środkowych AE I BD i jest środkową poprowadzoną do trzeciego boku. 2)

	1
EF||AC i |EF|=		|AC|
	2

	1
ΔEFP∼ΔACP w skali k=		⇔
	2

|PC|=2*|PF| i |AP|=2|PE| c.n.w ============

wifik: Dowód z trapezem to inny sposób na rozwiązanie tego niż pierwszy? Jesli tak to dziękuję bardzo!

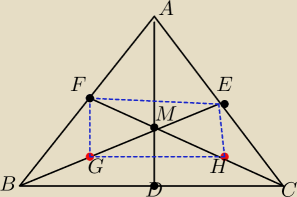
Krzysiek60: Twierdzenie Srodkowe trzech bokow trojkata przecinaja sie w jednym punkcie i odcinek srodkowej zawarty miiedzy tym punktem przeciecia i bokiem trojkata jest rowny trzeciej czesci srodkowej Zalozenie AD, BE CF sa srodkowymi bokow trojkata czyli AF= FB= EC i BD= DC Teza Ad BE CF przecinaja sie w jednym punkcie

	1		1
oraz MD=		AD ME=		BE MF= U{1}[3} CF
	3		3

Dowod dzielimy odcinki BM i CM na polowy i srodki tych odcinkow H i G oraz punkty F i E polaczymy kolejno odcinkami

	1
Odcinek FE laczy srodki dwoch bokow trojkata ABC wiec FE=		BCi FEIIBC
	2

Odcinek GH laczy srodki dwoch bokow trojkata BMC stad GH= U{1}[2}BCi GHII BC mamy stad z eodcinki FE i GH sa sobie rowne i do siebie rownolegle Dwie proste roronoelegledo trzecie sa do siebie rownolegle stad czworokat FEGH jest rownileglobokiem W rownolegloboku przekatne dziela sie na polowy ME= MG i odcinek MG= GB stad

	1		1
ME=		BE i MF=		CF
	3		3

Takie samo rozumowanie przeprpwadzimy w stosunku do innej pary srodkowych np BE i AD Dojdziemy do wniosku ze jedna z tych srodkowych odcina od drugiej odcinek rowny trzeciej czesci tej dlugosci

	1
Mamy stad ze srodkowa AD musi przechodzic przez punkt M i wtedy MD=		AD .
	3