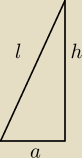 Na okręgu o promieniu r opisano trapez równoramienny ABCD o dłuższej podstawie AB i krótszej
CD. Punkt styczności S dzieli ramię trapezu tak, że
CS/SB = 2/5. Wyznacz długość ramienia trapezu i oblicz cos kąta CBD
Co do ramienia to:
CS = 2x, SB = 5x. Ze środka O okręgu poprowadziłem styczną na podstawy, więc AB = 10x, DC = 4x.
Wysokość trapezu: 2r = h. a = (10x−4x)/2 = 3x. Więc l mogę policzyć z tw. pitagorasa, tyle że
nie wiem co z tym x−em zrobić. Bo jego chyba trzeba jakoś inaczej wyrazić. Co do kąta to nie
mam pojęcia
Na okręgu o promieniu r opisano trapez równoramienny ABCD o dłuższej podstawie AB i krótszej
CD. Punkt styczności S dzieli ramię trapezu tak, że
CS/SB = 2/5. Wyznacz długość ramienia trapezu i oblicz cos kąta CBD
Co do ramienia to:
CS = 2x, SB = 5x. Ze środka O okręgu poprowadziłem styczną na podstawy, więc AB = 10x, DC = 4x.
Wysokość trapezu: 2r = h. a = (10x−4x)/2 = 3x. Więc l mogę policzyć z tw. pitagorasa, tyle że
nie wiem co z tym x−em zrobić. Bo jego chyba trzeba jakoś inaczej wyrazić. Co do kąta to nie
mam pojęcia
| √10 | ||
x = | r | |
| 10 |
| 7√10 | ||
7x = | r | |
| 10 |
| 122 | ||
Wyszło mi, że cosα = | − wynik dość dziwny i mam obawy czy poprawny | |
| 14*√89 |
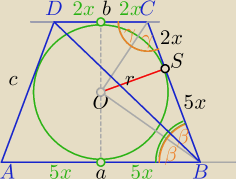 1)
środek okręgu wpisanego w wielokąt leży na przecięciu dwusiecznych kątów wewnętrznych.
2) suma kątów przy ramieniu trapezu wynosi 180o.
Stąd:
2β+2γ=180o
β+γ=90o⇒∡COB=90o ( suma kątów w Δ)
3) Wysokość opuszczona z wierzchołka kąta prostego dzieli przeciwprostokątną na odcinki
m i n takie, że : h2=m*n
(zapamiętaj!)
Zatem: r2=2x*5x⇔r2=10x2
1)
środek okręgu wpisanego w wielokąt leży na przecięciu dwusiecznych kątów wewnętrznych.
2) suma kątów przy ramieniu trapezu wynosi 180o.
Stąd:
2β+2γ=180o
β+γ=90o⇒∡COB=90o ( suma kątów w Δ)
3) Wysokość opuszczona z wierzchołka kąta prostego dzieli przeciwprostokątną na odcinki
m i n takie, że : h2=m*n
(zapamiętaj!)
Zatem: r2=2x*5x⇔r2=10x2
| r2 | ||
x2= | ||
| 10 |
| r | ||
x= | ||
| √10 |
| 7r | ||
|BC|= | ||
| √10 |

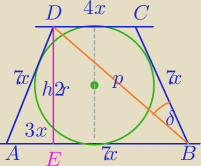 1)
h2=49x2−9x2=40x2
p2=h2+(7x)2=40x2+49x2
p2=89x2
2) Z tw. cosinusów w ΔDCB:
(4x)2=p2+(7x)2−2*p*7x*cosδ
16x2=89x2+49x2−14*√89x2*cosδ
122x2=14√89x2cosδ
1)
h2=49x2−9x2=40x2
p2=h2+(7x)2=40x2+49x2
p2=89x2
2) Z tw. cosinusów w ΔDCB:
(4x)2=p2+(7x)2−2*p*7x*cosδ
16x2=89x2+49x2−14*√89x2*cosδ
122x2=14√89x2cosδ
| 61 | ||
cosδ= | i to się zgadza z Twoim wynikiem | |
| 7√89 |

