środkowa
jolka: Mamy trójkat ABC i środkową BD. Punktami E i F dzielimy tę środkową na trzy równe części tak że
BE = EF = FD. Oblicz długość CE jeśli AB = 1 oraz AF = AD.
19 mar 16:05
ite:
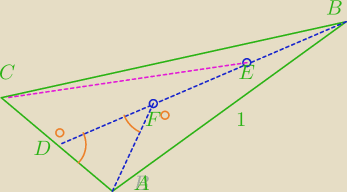
|BE|=|EF|=|FD|, |AB|=1
|CD|=|DA|, |AF|=|AD|
|CE|=?
|AF|=|AD| → ΔDFA równoramienny → |<FDA|=|<|DFA|
|<CDB|=180
o|−|<FDA|
|<AFB|=180
o|−|<DFA|
|<CDB|=|<AFB|
|CD|=|FA|
|DE|=|BF|=2*|FE|,
ΔCDE≡ΔAFB (bkb)
|CE|=|AB|=1
20 mar 11:26
Eta:
Pięknie Td ..


20 mar 12:43
ite:
o jak miło dostać i pochwałę i jabłko

20 mar 12:56
Eta:

20 mar 12:58
 |BE|=|EF|=|FD|, |AB|=1
|CD|=|DA|, |AF|=|AD|
|CE|=?
|AF|=|AD| → ΔDFA równoramienny → |<FDA|=|<|DFA|
|<CDB|=180o|−|<FDA|
|<AFB|=180o|−|<DFA|
|<CDB|=|<AFB|
|CD|=|FA|
|DE|=|BF|=2*|FE|,
ΔCDE≡ΔAFB (bkb)
|CE|=|AB|=1
|BE|=|EF|=|FD|, |AB|=1
|CD|=|DA|, |AF|=|AD|
|CE|=?
|AF|=|AD| → ΔDFA równoramienny → |<FDA|=|<|DFA|
|<CDB|=180o|−|<FDA|
|<AFB|=180o|−|<DFA|
|<CDB|=|<AFB|
|CD|=|FA|
|DE|=|BF|=2*|FE|,
ΔCDE≡ΔAFB (bkb)
|CE|=|AB|=1



