calki oznaczone spirner: Mam takie pytanko czy jest możliwość by w jakiś sposób zoptymalizować sumę 2 całek oznaczony np takich

	x
∫0a 1+xdx+∫b0 1−		dx gdzie a+b to odcinek o długości 1 w taki sposób by było
	6

największe pole

Adamm: tam powinny być nawiasy ∫_a⁰(1+x)dx+∫₀^b(1−x/6)dx co niby znaczy że a+b to odcinek o długości jeden? masz chyba na myśli odcinek [a, b], a<b ?

spirner: chodzi mi o to ze |a|+|b|=1 gdzie a<0 a b>0

spirner: a i b to niewiadome

Adamm: no to teraz inne zadanie...

spirner: bo z policzeniem całki nie mam problemu tylko z tym jak to ustawić by było największe pole

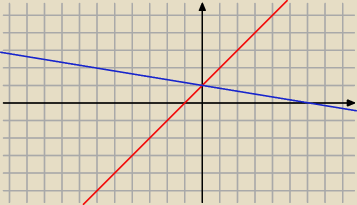
Adamm: 1. a≤0≤b widać że przyrost pola dla funkcji 1+x (−x+1 dla [0, 1]) jest mniejszy niż 1−x/6 (dla [0, 1]) czyli na pewno maksimum tutaj będzie dla b=1 i a=0 2. a≥0≥b tutaj całki będą ujemne, maksimum będzie niedodatnie, więc na pewno mniejsze 3. a, b≥0 im większe a, tym na pewno mniejsza całość (całka ujemna), i tym mniejsze b, więc druga całka też mniejsza, maksimum dla a=0, b=1 jak wcześniej 4. a, b≤0 tutaj ze wzrostem a całość jest mniejsza maksimum dla a=−1, b=0 czyli na pewno b=1, a=0 będzie największe

spirner: niestety ale nie jest to poprawna odpowiedz https://www.symbolab.com/solver/step-by-step/%5Cint_%7B0%7D%5E%7B0%7D%201%2Bxdx%2B%5Cint_%7B0%7D%5E%7B1%7D%201-%5Cfrac%7Bx%7D%7B6%7Ddx https://www.symbolab.com/solver/step-by-step/%5Cint_%7B-0.14%7D%5E%7B0%7D%201%2Bxdx%2B%5Cint_%7B0%7D%5E%7B0.86%7D%201-%5Cfrac%7Bx%7D%7B6%7Ddx wynik będzie gdzieś kolo a= −0,14 b=0,86 ale doszedłem do tego metodą prób i błędów a to nie jest najlepszy sposób gdy muszę zrobić takich przykładów jeszcze z 10 no nic dzięki za szczere chęci może ktoś inny ma jakiś sposób w jaki można by to sprawnie zoptymalizować

Pytający: Uzależniasz a od b (lub na odwrót): a=b−1 b∊<0,1> I liczysz całki oznaczone, wychodzi funkcja jednej zmiennej: ...=−7/12b²+b+1/2 https://www.wolframalpha.com/input/?i=(int+(b-1)..0+of+(1%2Bx)dx)%2B(int+0..b+of+(1-x%2F6)dx) Maksimum = 13/14 dla b=6/7, a=−1/7.