Planimetria
UczącySię: Długości boków trójkąta prostokątnego tworzą ciąg arytmetyczny o różnicy r> 0. R jest długością
promienia okręgu wpisanego w ten trójkąt. Wykaz, że r = R
Skorzystałem z własności ciągu arytmetycznego i wzoru na promień ale nie wyszło mi to
18 mar 22:33
Basia:
b − średni bok
a=b−r
c=b+r
(b+r)
2 = (b−r)
2+b
2
b
2+2br+r
2 = b
2−2br+r
2+b
2
4br = b
2
4r = b
a=3r
b=4r
c=5r
| | a+b−c | | 3r+4r−5r | |
R = |
| = |
| = r |
| | 2 | | 2 | |
18 mar 22:54
heheszek:
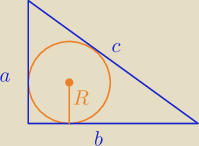
boki trojkata to a,b,c gdzie:
a, b=a+r, c = a+2r
| | 1 | | 1 | |
wiemy, ze |
| * a * b = |
| * R * (a+b+c) (bo to jest pole trojkata) |
| | 2 | | 2 | |
oraz ze a
2+b
2 = c
2 (pitagoras)
zatem
1)
| 1 | | 1 | |
| * a * (a+r) = |
| * R * (a+a+r+a+2r) |
| 2 | | 2 | |
a(a+r) = R(3a+3r)
a
2 + ar = 3aR + 3rR
2) a
2 + (a+r)
2 = (a+2r)
2
a
2 + a
2 +2ar + r
2 = a
2 + 4ar + 4r
2
a
2 − 2ar − 3r
2 = 0 −−> znajdz 'a' za pomoca 'r' (liczac delte)
i wrzuc do tego wzoru a
2 + ar = 3aR + 3rR
18 mar 22:57
UczącySię: Dzięki Basia ! Heheszek twoim sposobem też mi wyszło, bo jedno r jest ujemne
18 mar 23:02