zadania 3 i 5 z finału OMJ b: 3. Niech n będzie dodatnią liczbą całkowitą. Każdą z liczb 1,2,3,...,1000 pomalowano jednym z n kolorów. Okazało się, że każde dwie liczby, z których jedna jest dzielnikiem drugiej są pomalowane różnymi kolorami. Wyznacz najmniejszą liczbę n, dla której taka sytuacja jest możliwa. 5. Punkt M jest środkiem boku AB trójkąta równobocznego ABC. Punkty D i E leżą odpowiednio na odcinkach AC i BC,

	1
przy czym <)DME = 60◦. Wykaż, że AD +BE = DE +		AB
	2

Dałby ktoś jakieś wskazówki do tych zadań?

Blee: 3. Po pierwsze −−− wszystkie liczby pierwsze (i '1' ) są pomalowane na ten sam kolor Po drugie −−− wszystkie liczby postaci p*q (w tym także p²) ; gdzie p i q są pierwsze są pomalowane na ten sam (inny niż przy liczbach pierwszych) kolor Po trzecie −−− liczby postaci p*q*r (w tym także p²*q i p³) są pomalowane na trzeci kolor Itd. Należy zauważyć że 2¹⁰ = 1024 > 1000 Czyli wszystkie liczby da się pomalować na ile kolorów

Blee: tfu tfu ... 1 musi być na inny (osobny) kolor pomalowana −−− w końcu ona jest dzielnikiem każdej liczby

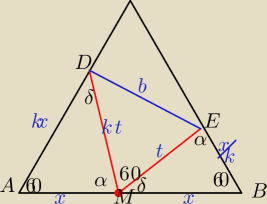
Basia: δ=180−60−α=120−α α+β+60=180 β=120−α=δ γ=180−60−120+α=α tr. AMD i tr.BEM sa podobne w skali k (na mocy cechy kkk) boki jak na rysunku

	x2		x
t2 = x2+		−2*x*		*U{1}[2}
	k2		k

	1		1		k2+1−k
t2 = x2(1+		−		) = x2*
	k2		k		k2

	1
b2 = t2+k2t2−2t*kt*		= t2(1+k2−k) =
	2

	k2+1−k		(k2+1−k)2
x2*		*(k2+1−k) = x2*
	k2		k2

	k2+1−k		x
b = x*		= x*(k + U{1}[k} −1) = kx +		− x
	k		k

	1
DE = AD + BE −		AB
	2

	1
AD+BE = DE+		AB
	2

c.b.d.o.