Planimetria UczącySię: W trójkącie ABC dane są długości boków a i b. Oblicz długość trzeciego boku jeśli wiadomo że kąt C jest dwa razy większy od kąta B. Mi wyszło

	a−bcos2α
c=		ale to zła odpowiedz. Zastosowałem twierdzenie cosinusów. Proszę o pomoc
	cosα

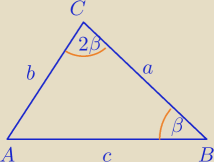
Mila: 1) porównanie pól

	1
PΔ=		*a*b*sin2β
	2

	1
PΔ=		*a*c*sinβ⇔
	2

1		1
	*a*b*sin2β=		*a*c*sinβ
2		2

b*2sinβ*cosβ=c*sinβ c=2bcosβ

	c
cosβ=
	2b

2) Tw. cosinusów b²=c²+a²−2ac*cosβ

	c
b2=c2+a2−2*a*c*
	2b

	c2*a
b2=c2+a2−		/*b
	b

b³=bc²+a²b−ac² b³−a²b=c²*(b−a) b*(b²−a²)=c²*(b−a) , b*(b−a)*(b+a)=c²*(b−a) dla b≠a c²=b*(a+b) c=√a*(a+b)

Mila: Rozważ przypadek: Dla a=b

UczącySię: Dziękuję Milu ! Jak ty na to wszystko "o tak" wpadasz ?

Eta:

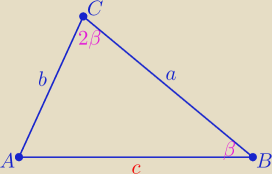
	ac*sinβ		ab*sin2β)
1/ P(ABC)=		i P(ABC)=
	2		2

	a
to acsinβ= ab*2sinβ*cosβ ⇒ cosβ=
	2b

z tw. cosinusów : b²=c²+a²−2ac*cosβ

	ac2
b2=c2+a2−		/*b
	b

b³−a²b= bc²−ac² b(b²−a²)= c²(b−a) /: (b−a , b>a b(b+a)=c² c=√b(a+b =========

Eta: I na darmo pisałam

UczącySię: Milu jeśli a = b to dostałem, że cosB=c/2a i wtedy c² = 2ac * c/2a czyli 0=0

Mila: Eta Nie na darmo, bo wyniki się zgadzają. Uczący Dla a=b jest to Δprostokatny równoramienny i też będzie dobrze.

Basia: UczącySię dla a=b kąt A = β i masz 4β=180 β=45 2β=90 c² = a²+b² = 2a² c = a√2 Mila wyprowadziła wzór c = √a(a+b) b=a i masz c = √a*2a = √2a² = a√2

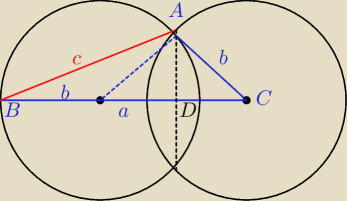
an: może tak wystarczy Pitagoras ∡C=2∡B wynika z własnośi kątów w kole

	a−b		a−b
AD2=c2−((		+b)2=b2 −(		)2
	2		2

c²=ab+b² c=√b(a+b)