planimetria blehh: na czworokącie ABCD opisano okrąg o(O,r). Dwusieczna kąta bad przecina okrąg w punkcie K, zaś dwusieczna kąta BCD przecina okrąg w punkcie L. Wykaż, że punkty K, L, O są współliniowe. Rysunek: https://snag.gy/WRE8jo.jpg

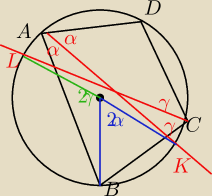
Basia: 2α+2γ=180 z warumku dla czworokata wpisanego w okrąg kąt KOB = 2α bo jest oparty na tym samym łuku co kąt wpisany BAK kąt LOB = 2γ bo jest oparty na tym samym łuku co kąt wpisany LCB czyli LOB+BOK = 2α+2γ=190 ⇒ L,O,B są współliniowe

aniabb: http://prntscr.com/it1wnn a skoro wpisany w okrąg to suma kątów naprzeciwko =180° czyli 2α+2β=180° czyli KOL są jedną linią